题目内容
5. 如图,水平传送带上表面的右侧,与一个竖直的光滑半圆轨道底端相接,在半圆轨道下端O放一质量为m的滑块A,传送带以速率v0沿顺时针转动,现在传送带的左端轻轻放上一个质量也为m的滑块B,物块与传送带的动摩擦因数为μ,物块B以速度为v0与A发生弹性碰撞,物块脱离轨道飞出后落在轨道或传送带上将会继续发生碰撞,两滑块可视为质点,求:
如图,水平传送带上表面的右侧,与一个竖直的光滑半圆轨道底端相接,在半圆轨道下端O放一质量为m的滑块A,传送带以速率v0沿顺时针转动,现在传送带的左端轻轻放上一个质量也为m的滑块B,物块与传送带的动摩擦因数为μ,物块B以速度为v0与A发生弹性碰撞,物块脱离轨道飞出后落在轨道或传送带上将会继续发生碰撞,两滑块可视为质点,求:(1)传送带至少多长?
(2)要保证被撞后的A滑块能沿圆弧轨道运动,圆弧轨道的半径应满足什么条件?
(3)若A与B能在O点发生多次碰撞,则当A与B发生第五次碰撞时,物块与传送带间的摩擦产生的内能是多少?
分析 (1)由牛顿第二定律求出物体B的加速度,当达到传送带速度时物体B前进的位移即为传送带的长度;
(2)物块B以速度为v0与A发生弹性碰撞,根据动量定理求的物体A的速度,由牛顿第二定律求的到达最高点的速度,由动能定理求的半径;
(3)求出在每一次碰撞过程中物体B与传送带的相对位移,由Q=μmgx求得产生的内能,即可求得在当A与B发生第五次碰撞时,物块与传送带间的摩擦产生的内能
解答 解:(1)物块B在传送带上加速运动,由牛顿第二定律可知μmg=ma
a=μg
加速到与传送带具有相同速度前进的位移为x=$\frac{{v}_{0}^{2}}{2a}=\frac{{v}_{0}^{2}}{2μg}$
(2)根据动量定理,碰撞后A的速度为v0
物体到达圆弧最高点具有的速度为
mg=$m\frac{{v}^{2}}{R}$
v=$\sqrt{gR}$
从A到B由动能定理可得
-2mgR=$\frac{1}{2}m{v}^{2}-\frac{1}{2}{mv}_{0}^{2}$
解得R=$\frac{{v}_{0}^{2}}{5g}$
半径最大为$\frac{{v}_{0}^{2}}{5g}$
(3)若A与B能在O点发生多次碰撞,
物块B第一次在传送带上运动达到传送带速度所需时间为t1=$\frac{{v}_{0}}{μg}$
物块B前进的位移为x1=$\frac{1}{2}{at}_{1}^{2}$=$\frac{{v}_{0}^{2}}{2μg}$
传送带前进的位移为x2=v0t1=$\frac{{v}_{0}^{2}}{μg}$,相对位移$△{x}_{1}={x}_{2}-{x}_{1}=\frac{{v}_{0}^{2}}{2μg}$
产生的内能为${Q}_{1}=μmg•△{x}_{1}=\frac{1}{2}{mv}_{0}^{2}$
第一次与A发生碰撞后A沿向上运动后再沿圆弧下滑,与B发生第二次碰撞,物体B在传送带上做减速运动,减速运动到零物体B与传送带的相对位移为
$△{x}_{2}={x}_{2}+{x}_{1}=\frac{3{v}_{0}^{2}}{2μg}$
产生的内能为${Q}_{2}=μmg•△{x}_{2}=\frac{3}{2}{mv}_{0}^{2}$
依此类推当第五次发生碰撞时产生的总内能为$Q=3{Q}_{1}+2{Q}_{2}=\frac{9}{2}{mv}_{0}^{2}$
答:(1)传送带至少为$\frac{{v}_{0}^{2}}{2μg}$
(2)要保证被撞后的A滑块能沿圆弧轨道运动,圆弧轨道的半径最大为$\frac{{v}_{0}^{2}}{5g}$
(3)块与传送带间的摩擦产生的内能是$\frac{9}{2}{mv}_{0}^{2}$
点评 本题主要考查了匀加速度直线运动与动能定理,抓住运动过程是关键;

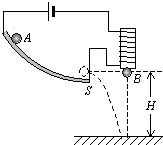 在研究平抛运动时,为证明平抛运动竖直方向的分运动是自由落体运动.某同学设计了如图所示的实验装置:小球A沿轨道滑下,离开轨道末端时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落,发现位于同一高度的A、B两球总是同时落地.该现象说明了A球在离开轨道后,竖直方向的分运动是自由落体运动.下面列出了一些操作要求,你认为正确的是( )
在研究平抛运动时,为证明平抛运动竖直方向的分运动是自由落体运动.某同学设计了如图所示的实验装置:小球A沿轨道滑下,离开轨道末端时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落,发现位于同一高度的A、B两球总是同时落地.该现象说明了A球在离开轨道后,竖直方向的分运动是自由落体运动.下面列出了一些操作要求,你认为正确的是( )| A. | 通过调节轨道,必须使轨道末端水平 | |
| B. | 通过调节整个装置,使A球离开轨道末端时与B球从同一高度下落 | |
| C. | 每次在轨道上端释放小球A的位置必须在同一点 | |
| D. | 每次在轨道上端释放小球A,必须由静止释放 | |
| E. | 必须改变整个装置的高度H做同样的实验 | |
| F. | 换用更加光滑的轨道重做试验,结果会更精确 |
| A. | 瞬时速度是指物体在某一位置或某一时刻的速度 | |
| B. | 平均速度是物体在一段时间内位移与所用时间的比值 | |
| C. | 做变速运动的物体,平均速率就是平均速度的大小 | |
| D. | 物体做变速运动时,平均速度是指物体通过的路程与所用时间的比值 |
 “嫦娥三号”从距月面高度为100km的环月圆轨道I上的P点实施变轨,进入近月点为15km的椭圆轨道Ⅱ,由近月点Q成功落月,如图所示.关于“嫦娥三号”,下列说法正确的是( )
“嫦娥三号”从距月面高度为100km的环月圆轨道I上的P点实施变轨,进入近月点为15km的椭圆轨道Ⅱ,由近月点Q成功落月,如图所示.关于“嫦娥三号”,下列说法正确的是( )| A. | 沿轨道I运动至P时,需加速才能进入轨道Ⅱ | |
| B. | 沿轨道Ⅱ运行的周期大于沿轨道I运行的周期 | |
| C. | 沿轨道Ⅱ运行时,在P点的加速度小于在Q点的加速度 | |
| D. | 在轨道Ⅱ上由P点运行到Q点的过程中,万有引力对其做负功 |
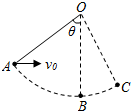 如图,一个小球可以绕O点在竖直面内做圆周运动,B点是圆周运动的最低点,悬线的长为L,现将球拉至A点,悬线刚好拉直,悬线与竖直方向的夹角为53°,给小球一个水平向右的初速度,结果小球刚好能到达C点,小球的质量为m,重力加速速度为g,求:(sin53°=0.8,cos53°=0.6)
如图,一个小球可以绕O点在竖直面内做圆周运动,B点是圆周运动的最低点,悬线的长为L,现将球拉至A点,悬线刚好拉直,悬线与竖直方向的夹角为53°,给小球一个水平向右的初速度,结果小球刚好能到达C点,小球的质量为m,重力加速速度为g,求:(sin53°=0.8,cos53°=0.6) 如图所示,重力大小为G的小姑娘从倾角为θ的滑梯上匀速滑下.则斜面对小姑娘的支持力N=Gcosθ,她受到的摩擦力f=Gsinθ.
如图所示,重力大小为G的小姑娘从倾角为θ的滑梯上匀速滑下.则斜面对小姑娘的支持力N=Gcosθ,她受到的摩擦力f=Gsinθ.