题目内容
13.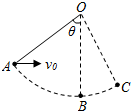 如图,一个小球可以绕O点在竖直面内做圆周运动,B点是圆周运动的最低点,悬线的长为L,现将球拉至A点,悬线刚好拉直,悬线与竖直方向的夹角为53°,给小球一个水平向右的初速度,结果小球刚好能到达C点,小球的质量为m,重力加速速度为g,求:(sin53°=0.8,cos53°=0.6)
如图,一个小球可以绕O点在竖直面内做圆周运动,B点是圆周运动的最低点,悬线的长为L,现将球拉至A点,悬线刚好拉直,悬线与竖直方向的夹角为53°,给小球一个水平向右的初速度,结果小球刚好能到达C点,小球的质量为m,重力加速速度为g,求:(sin53°=0.8,cos53°=0.6)(1)小球的初速度大小;
(2)小球在B点开始做圆周运动时绳的张力;
(3)小球运动到B点时绳绷紧过程损失的机械能及小球向右运动到的最高点C相对于B点的高度.
分析 (1)小球由A到B做平抛运动,根据平抛运动规律即可解的
(2)对BC过程,根据动能定理解B点速度,根据合力充当向心力列式求解绳子的张力
(3)根据平抛运动规律求解末速度大小,根据能量守恒定律绳绷紧过程损失的机械能;对BC过程由机械能守恒定律可求得高度.
解答 解:(1)小球由A到B做平抛运动
根据平抛运动规律知
Lsin53°=v0t
L(1-cos53°)=$\frac{1}{2}g{t}^{2}$
联立上式解得 t=$\sqrt{\frac{4L}{5g}}$,v0=$\sqrt{\frac{4}{5}gL}$
(2)根据运动的合成和分解知:小球到达B点绳绷紧前瞬间的速度大小为 v=$\sqrt{{v}_{0}^{2}+(gt)^{2}}$
速度与水平方向的夹角为α,则tanα=$\frac{gt}{{v}_{0}}$=1,α=45°
则绳绷紧后瞬间小球的速度为 v′=v0tanα=$\sqrt{\frac{4}{5}gL}$
在B点,有 T-mg=m$\frac{v{′}^{2}}{L}$,解得 T=1.8mg
(3)小球运动到B点时绳绷紧过程损失的机械能△E=$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}m{v}_{\;}^{′2}$=$\frac{2}{5}$mgL
设小球向右运动到的最高点C相对于B点的高度为h,由机械能守恒定律可知:
mgh=$\frac{1}{2}$mv'2
解得:h=$\frac{v{′}^{2}}{2g}$=$\frac{\frac{4}{5}gL}{2×g}$=$\frac{2}{5}$L;
答:(1)小球的初速度大小为$\sqrt{\frac{4}{5}gL}$;
(2)小球在B点开始做圆周运动时绳的张力为1.8mg;
(3)小球运动到B点时绳绷紧过程损失的机械能为$\frac{2}{5}$mgL;小球向右运动到的最高点C相对于B点的高度$\frac{2}{5}$L.
点评 本题考查能量的转化及守恒关系,要注意确定物理过程,明确在绳子绷紧的过程中会有能量损失.

 阅读快车系列答案
阅读快车系列答案| A. | T=$\frac{{t}_{2}-{t}_{1}}{n}$ | B. | T=$\frac{{t}_{1}-{t}_{2}}{n}$ | C. | T=$\frac{2πr}{v}$ | D. | T=$\frac{2πv}{r}$ |
 2014年9月26日,印度火星探测器成功进入X星近地面轨道,其匀速圆周运动运动周期为T,已知火星半径为r,火星表面重力加速度为g,X有引力常量为G,则
2014年9月26日,印度火星探测器成功进入X星近地面轨道,其匀速圆周运动运动周期为T,已知火星半径为r,火星表面重力加速度为g,X有引力常量为G,则( )
| A. | 火星的质量可表述为$\frac{{r}^{2}}{gG}$ | |
| B. | 火星的质量可表述为$\frac{4{r}^{2}}{G{T}^{2}}$ | |
| C. | 火星表面第一宇宙速度可表述为$\sqrt{gr}$ | |
| D. | 火星探测器若准备火星着陆,应向后喷气改变运行轨道 |
| A. | 动能、重力势能和机械能逐渐减小 | |
| B. | 重力势能逐渐减小,动能逐渐增大,机械能不变 | |
| C. | 重力势能逐渐增大,动能逐渐减小,机械能不变 | |
| D. | 重力势能逐渐减小,动能逐渐增大,机械能逐渐减小 |
 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电荷q的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电荷q的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,a的电势最高 | |
| B. | 带电质点通过P点时的加速度较Q点大 | |
| C. | 带电质点通过P点时的动能较Q点大2qUab | |
| D. | 带电质点通过P点时的电势能较Q点大2qUab |
| A. | 重力就是地球对物体的吸引力 | |
| B. | 重力是由于物体受到地球的吸引而产生的 | |
| C. | 只有静止的物体才受到重力 | |
| D. | 重力G跟质量m的关系式G=mg中,g一定等于9.8m/s2 |

 如图所示,虚线上方空间有垂直线框平面的匀强磁场,直角扇形导线框绕垂直于线框平面的轴O以角速度ω匀速转动.设线框中感应电流方向以逆时针为正,那么在选项中能正确描述线框从图中所示位置开始转动一周的过程中,线框内感应电流随时间变化情况的是( )
如图所示,虚线上方空间有垂直线框平面的匀强磁场,直角扇形导线框绕垂直于线框平面的轴O以角速度ω匀速转动.设线框中感应电流方向以逆时针为正,那么在选项中能正确描述线框从图中所示位置开始转动一周的过程中,线框内感应电流随时间变化情况的是( )



 如图,水平传送带上表面的右侧,与一个竖直的光滑半圆轨道底端相接,在半圆轨道下端O放一质量为m的滑块A,传送带以速率v0沿顺时针转动,现在传送带的左端轻轻放上一个质量也为m的滑块B,物块与传送带的动摩擦因数为μ,物块B以速度为v0与A发生弹性碰撞,物块脱离轨道飞出后落在轨道或传送带上将会继续发生碰撞,两滑块可视为质点,求:
如图,水平传送带上表面的右侧,与一个竖直的光滑半圆轨道底端相接,在半圆轨道下端O放一质量为m的滑块A,传送带以速率v0沿顺时针转动,现在传送带的左端轻轻放上一个质量也为m的滑块B,物块与传送带的动摩擦因数为μ,物块B以速度为v0与A发生弹性碰撞,物块脱离轨道飞出后落在轨道或传送带上将会继续发生碰撞,两滑块可视为质点,求: