题目内容
8．
一个初始质量为1kg的玩具火箭被竖直发射到空中，它的质量以0.2kg/s的恒定速率减小，火箭最终质量为0.2kg，喷出的气体对火箭的推力随时间变化的规律如图所示，火箭所经处的重力加速度恒为g=10m/s2，（1）求出重力随时间变化的表达式？
（2）在图中作出火箭的重力随时间变化的规律图象并求出火箭离开地面的时间t？．
（3）求4s时火箭的速度是多大？
分析 （1、2）火箭的质量均匀减小，求得火箭的质量与时间的关系，即可求得火箭的重力与时间的关系，当火箭的推力大于重力时，火箭离开地面，根据图象即可判断；
（3）在图象中，找出合力的冲量，根据冲量定理求得末速度．
解答 
解：（1）火箭的质量m=M-0.2t
故火箭的重力G=mg=Mg-0.2gt=10-2t，
（2）图象如图所示：
当推力大于重力时，火箭开始离开地面，故由图象可知，在t=0.55s离开地面；
（2）由图线所围面积可知合力的冲量为31N•s
根据冲量定理可知v=$\frac{P}{m}$=$\frac{31}{0.2}$=155m/s．
答：（1）重力随时间变化的表达式为mg=10-2t；
（2）火箭的重力随时间变化的规律如图所示，火箭在0.55s时候离开地面；
（3）t=4s时火箭的速度为155m/s．
点评 本题主要考查了图象问题，根据题意很简单的找出火箭的重力与时间的关系，在第二问中，关键是利用好图象求得合力的冲量．
练习册系列答案
相关题目
19．光敏电阻能将光信号转化为电信号是因为（ ）
| A． | 光照强度发生变化时，光敏电阻的阻值也发生变化 | |
| B． | 光照强度发生变化时，光敏电阻的体积也发生变化 | |
| C． | 光照强度发生变化时，光敏电阻的长度也发生变化 | |
| D． | 光照照度发生变化时，光敏电阻的横截面积也发生变化 |
16．
如图所涉及，正三角形ABC区域内存在匀强磁场，磁感应强度为B=$\frac{2\sqrt{3}m{v}_{0}}{3qL}$，△ABC边长为L，O为BC边的中点，大量质量为m，速度为v0的粒子从O点沿不同的方向垂直于磁场射入该磁场区域（不计粒子重力），则对于从AB和AC边射出的粒子在磁场中的运动时间不可能为（ ）
如图所涉及，正三角形ABC区域内存在匀强磁场，磁感应强度为B=$\frac{2\sqrt{3}m{v}_{0}}{3qL}$，△ABC边长为L，O为BC边的中点，大量质量为m，速度为v0的粒子从O点沿不同的方向垂直于磁场射入该磁场区域（不计粒子重力），则对于从AB和AC边射出的粒子在磁场中的运动时间不可能为（ ）| A． | $\frac{\sqrt{3}πL}{6{v}_{0}}$ | B． | $\frac{\sqrt{3}πL}{9{v}_{0}}$ | C． | $\frac{\sqrt{3}πL}{12{v}_{0}}$ | D． | $\frac{\sqrt{3}πL}{15{v}_{0}}$ |
3．
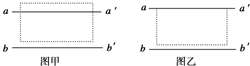在利用插针法测定玻璃砖折射率的实验中：甲同学在纸上正确画出玻璃砖的两个界面aa′和bb′后，不小心碰了玻璃砖使它向aa′方向平移了少许，如图甲所示．乙同学在画界面时，不小心将两界面aa′、bb′间距画得比玻璃砖宽度大些，如图乙所示，则（ ）
在利用插针法测定玻璃砖折射率的实验中：甲同学在纸上正确画出玻璃砖的两个界面aa′和bb′后，不小心碰了玻璃砖使它向aa′方向平移了少许，如图甲所示．乙同学在画界面时，不小心将两界面aa′、bb′间距画得比玻璃砖宽度大些，如图乙所示，则（ ）| A． | 甲测得折射率偏大，乙测得折射率偏小 | |
| B． | 甲测得折射率偏小，乙测得折射率不变 | |
| C． | 甲测得折射率不变，乙测得折射率偏小 | |
| D． | 甲测得折射率不变，乙测得折射率不变 |
13．已知食盐（NaCl）的密度为ρ，摩尔质量为M，阿伏伽德罗常数为NA，求：
①食盐分子的质量m=$\frac{M}{{N}_{A}}$
②食盐分子的体积V0=$\frac{M}{ρ{N}_{A}}$．
①食盐分子的质量m=$\frac{M}{{N}_{A}}$
②食盐分子的体积V0=$\frac{M}{ρ{N}_{A}}$．
20．以初速度竖直向上抛出一物体，空气阻力大小不变．关于物体受到的冲量，以下说法正确的是（ ）
| A． | 物体上升阶段和下落阶段受到的重力的冲量方向相反 | |
| B． | 物体上升阶段和下落阶段受到空气阻力冲量的大小相等 | |
| C． | 物体在下落阶段受到重力的冲量小于上升阶段受到重力的冲量 | |
| D． | 物体从抛出到返回抛出点，动量变化的方向向下 |
如图所示为一架小型四旋翼无人机，它是一种能够垂直起降的小型遥控飞行器，目前正得到越来越广泛的应用．无人机的质量为m=2kg，假定运动过程中所受空气阻力大小恒为f=4N，当无人机在地面上从静止开始，以最大升力竖直向上起飞，经时间t=4s时，离地面的高度为h=48m，g取10m/s2．