题目内容
1.如图甲所示,直角坐标系xoy中,第二象限内有沿x轴正方向的匀强电场.第一、四象限内有垂直坐标平面的匀强交变磁场.磁场方向垂直纸面向外为正方向.第三象限内有一发射装置(没有画出)沿y轴正方向射出一个比荷$\frac{q}{m}$=100C/kg的带正电的粒子,(可视为质点且不计重力),该粒子以v0=10m/s的速度从x轴上的点A(-1m.0)进入第二象限.从y轴上的点C(0,2m)进入第一象限.取粒子刚进入第一象限的时刻为0时刻,第一、四象限内磁场的磁感应强度按图乙所示规律变化.g=10m/s2
(1)求第二象限内电场的电场强度大小;
(2)求粒子第一次经过x轴时的位置坐标;
(3)若保持第一、四象限内的磁场大小不变,使其周期变为T0=$\frac{3π}{80}$s,该粒子的运动轨迹与x轴的交点坐标.
分析 (1)根据动能定理及类平抛运动的规律求解
(2)粒子在交变磁场中做匀速圆周运动,洛伦兹力提供向心力,求出半径和周期,根据几何关系求出交点坐标
(3)画出轨迹,考虑周期性,结合几何关系求交点坐标
解答 解:(1)带电粒子在第二象限的电场中做类平抛运动,设粒子从A点到C点用时为t,则
$Eq\\{x}_{A}^{\;}\\$$|{x}_{A}^{\;}|$=$\frac{1}{2}m({v}_{C}^{2}-{v}_{0}^{2})$
$|{x}_{A}^{\;}|=\frac{{v}_{Cx}^{\;}}{2}t$
${y}_{C}^{\;}={v}_{0}^{\;}t$
${v}_{C}^{2}={v}_{0}^{2}+{v}_{Cx}^{2}$
解得:E=0.5N/C ${v}_{C}^{\;}=10\sqrt{2}m$
(2)设粒子在C点的运动方向与y轴正方向成θ角,则
$cosθ=\frac{{v}_{0}^{\;}}{{v}_{C}^{\;}}=\frac{\sqrt{2}}{2},即θ=45°$
粒子在第一象限磁场中运动时$q{v}_{C}^{\;}B=m\frac{{v}_{C}^{2}}{r}$
解得$r=\frac{\sqrt{2}}{4}m$
粒子做圆周运动的周期$T=\frac{2πr}{{v}_{C}^{\;}}=\frac{π}{20}s$
所示粒子在磁场中的运动轨迹如图甲所示,粒子运动第四个半圆的过程中第一次经过x轴,在x轴上对应的弦长为$r\sqrt{2}$
所以$OD=2m-r\sqrt{2}$=1.5m
粒子第一次经过x轴时的位置坐标为(1.5m,0)
(3)在磁场变化的前半个周期内,设粒子偏转的角度为β,则
$β=\frac{2π}{T}×\frac{{T}_{0}^{\;}}{2}=\frac{3π}{4}$
在该段时间内粒子沿y轴负方向运动的距离$△y=rsinθ=\frac{1}{4}m$,沿x轴正方向运动的距离为
$△x=r(1+cosθ)=\frac{\sqrt{2}+1}{4}m$
因为$\frac{{y}_{C}^{\;}}{△y}=8$,所以粒子运动轨迹如图乙所示,粒子在磁场变化的第8个半周期和第9个半周期内共经过x轴3次
第1次:${x}_{1}^{\;}=8△x-2rcosθ=(2\sqrt{2}+\frac{3}{2})m$
第2次:${x}_{2}^{\;}=8△x=(2\sqrt{2}+2)m$
第3次:${x}_{3}^{\;}=8△x+2rcosθ=(2\sqrt{2}+\frac{5}{2})m$
答:(1)第二象限内电场的电场强度大小0.5N/C;
(2)粒子第一次经过x轴时的位置坐标(1.5m,0);
(3)若保持第一、四象限内的磁场大小不变,使其周期变为T0=$\frac{3π}{80}$s,该粒子的运动轨迹与x轴的交点坐标${x}_{1}^{\;}=(2\sqrt{2}+\frac{3}{2})m$,${x}_{2}^{\;}=(2\sqrt{2}+2)m$,${x}_{3}^{\;}=(2\sqrt{2}+\frac{5}{2})m$.
点评 本题中质点在复合场运动,分析受力情况,确定质点的运动情况是解题的基础.结合粒子运动的周期性,运用数学几何知识综合求解.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | 2倍之上 | B. | 10倍之上 | C. | 100倍之上 | D. | 1000倍之上 |
 如图所示,质量为1kg的小球从距地面H=1.6m的A点水平抛出,恰好垂直撞在水平面上半径为1m的半圆形物体上的B点,已知O为半圆的圆心,BO与竖直方向间的夹角为37°,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法正确的是( )
如图所示,质量为1kg的小球从距地面H=1.6m的A点水平抛出,恰好垂直撞在水平面上半径为1m的半圆形物体上的B点,已知O为半圆的圆心,BO与竖直方向间的夹角为37°,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法正确的是( )| A. | O与A点间的水平距离为2m | B. | 小球平抛的初速度v0为3m/s | ||
| C. | 小球到B点时重力的瞬时功率为40W | D. | 小球从A到B的运动时间为0.4s |
 如图所示,半圆形凹槽的半径为R,O点为其圆心,在与O点等高的边缘A、B两点分别以速度v1、v2水平相向同时抛出两个小球,两小球恰好在弧面上的P点相遇,∠AOP为60°,则以下说法中正确的是( )
如图所示,半圆形凹槽的半径为R,O点为其圆心,在与O点等高的边缘A、B两点分别以速度v1、v2水平相向同时抛出两个小球,两小球恰好在弧面上的P点相遇,∠AOP为60°,则以下说法中正确的是( )| A. | 两小球位移之比为1:3 | B. | 两小球初速度之比为v1:v2=1:3 | ||
| C. | 两小球相遇时速度大小之比为1:$\sqrt{3}$ | D. | 两小球的速度增加量之比为1:$\sqrt{3}$ |
 如图所示,大型露天游乐场中,翻滚过山车质量为1t,从轨道一侧的顶端A处由静止释放,到达底部B后又冲上环形轨道,使乘客头朝下通过C点,再沿环形轨道到底部,最后冲上轨道另一侧的顶点D.如果不考虑车与轨道间的摩擦和空气阻力,已知轨道的最高点A比最低点B高20m,圆环半径为5m(g取10m/s2).求:
如图所示,大型露天游乐场中,翻滚过山车质量为1t,从轨道一侧的顶端A处由静止释放,到达底部B后又冲上环形轨道,使乘客头朝下通过C点,再沿环形轨道到底部,最后冲上轨道另一侧的顶点D.如果不考虑车与轨道间的摩擦和空气阻力,已知轨道的最高点A比最低点B高20m,圆环半径为5m(g取10m/s2).求: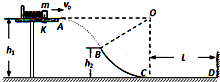 如图,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁定.现接触锁定,小物块与弹簧分离后将以一定的水平速度v0向右从A点滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与长L=2.8m的水平粗糙直轨道CD平滑连接,小物块恰能到达D处.重力加速度g=10m/s2,空气阻力忽略不计.求:
如图,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁定.现接触锁定,小物块与弹簧分离后将以一定的水平速度v0向右从A点滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与长L=2.8m的水平粗糙直轨道CD平滑连接,小物块恰能到达D处.重力加速度g=10m/s2,空气阻力忽略不计.求:
 滑块A、B与C点位于一条直线上,设A、B质量均为m且可视为质点,A、B间的距离为L,B与C点间距离为S,给A-瞬时初速度v0,使A向B运动并发生对心正碰,碰撞时间极短,碰撞过程中没有能量损失,设A、B与平面的动摩擦因数为μ.求:为使B通过C点,A的初速度v0最小是多大?
滑块A、B与C点位于一条直线上,设A、B质量均为m且可视为质点,A、B间的距离为L,B与C点间距离为S,给A-瞬时初速度v0,使A向B运动并发生对心正碰,碰撞时间极短,碰撞过程中没有能量损失,设A、B与平面的动摩擦因数为μ.求:为使B通过C点,A的初速度v0最小是多大?