题目内容
16.某同学在做“利用单摆测重力加速度”的实验中,先测得摆线长为L,摆球直径为d,然后用秒表记录了单摆全振动n次所用的时间为t.则:(1)他测得的重力加速度g=$\frac{4{π}^{2}{n}^{2}(L+\frac{1}{2}d)}{{t}^{2}}$.(用测量量表示)
(2)某同学在利用单摆测定重力加速度的实验中,若测得的g值偏大,可能的原因是E
A.摆球质量过大
B.单摆振动时振幅较小
C.测量摆长时,只考虑了线长忽略了小球的半径
D.测量周期时,把n个全振动误认为(n-1)个全振动,使周期偏大
E.测量周期时,把n个全振动误认为(n+1)个全振动,使周期偏小
(3)为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出一组对应的l和T的数值,再以l为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率K.则重力加速度g=$\frac{4{π}^{2}}{K}$.(用K表示)
(4)实验中游标尺(20分度)和秒表的读数如图,分别是18.95 mm、99.8 s.

分析 (1)由实验摆长和运动时间得到周期,再通过单摆周期公式联立解得重力加速度;
(2)根据重力加速度表达式判断各影响因素,进而得到g增大的可能原因;
(3)通过(1)中的重力加速度表达式,将K代入其中即可求解;
(4)按照游标卡尺和秒表的读数法,先读主尺和秒表小圈的分针数,然后再加上分尺和大圈秒针数即可.
解答 解:(1)该实验单摆摆长$l=L+\frac{1}{2}d$,周期$T=\frac{t}{n}$;故由单摆运动周期$T=2π\sqrt{\frac{l}{g}}$可得$g=\frac{4{π}^{2}l}{{T}^{2}}$=$\frac{4{π}^{2}{n}^{2}(L+\frac{1}{2}d)}{{t}^{2}}$;
(2)由(1)可知,g与摆球质量、单摆振动时振幅无关,且若测得的g值偏大,则l偏大或T偏小;那么,测量摆长时,只考虑了线长忽略了小球的半径,则l偏小,g偏小;故可能原因为E;
(3)以l为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率K,那么$\frac{l}{{T}^{2}}=\frac{1}{K}$,所以,$g=\frac{4{π}^{2}l}{{T}^{2}}=\frac{4{π}^{2}}{K}$;
(4)游标卡尺的读数为18mm+19×0.05mm=18.95mm,秒表的读数为1.5×60s+9.8s=99.8s;
故答案为:(1)$\frac{4{π}^{2}{n}^{2}(L+\frac{1}{2}d)}{{t}^{2}}$;(2)E;(3)$\frac{4{π}^{2}}{K}$;(4)18.95mm,99.8s.
点评 实验题一般根据实验应用原理分析实验中的测量量,然后进行各测量量对实验值的误差影响.

练习册系列答案
相关题目
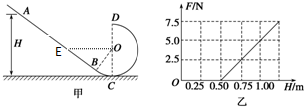
6.如图甲所示,竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成,AB和BCD相切于B点,CD连线是圆轨道竖直方向的直径(C、D为圆轨道的最低点和最高点),已知∠BOC=30°.可视为质点的小滑块从轨道AB上高H处的某点由静止滑下,用力传感器测出小滑块经过圆轨道最高点D时对轨道的压力为F,并得到如图乙所示的压力F与高度H的关系图象,取g=10m/s2.则( )

| A. | 圆轨道的半径为0.2m | |
| B. | 无法计算出小滑块的质量 | |
| C. | H取合适的值,可以使得小滑块经过最高点D后直接落到轨道AB上与圆心O等高的E点 | |
| D. | 由图乙可知,若H<0.50m,小滑块一定会在运动到D点之前脱离轨道 |
11. 如图所示,重为G的物体静止在倾角为α的粗糙斜面体上,现使斜面体向右做匀速直线运动,通过的位移为x,物体相对斜面体一直保持静止,则在这个过程中( )
如图所示,重为G的物体静止在倾角为α的粗糙斜面体上,现使斜面体向右做匀速直线运动,通过的位移为x,物体相对斜面体一直保持静止,则在这个过程中( )
 如图所示,重为G的物体静止在倾角为α的粗糙斜面体上,现使斜面体向右做匀速直线运动,通过的位移为x,物体相对斜面体一直保持静止,则在这个过程中( )
如图所示,重为G的物体静止在倾角为α的粗糙斜面体上,现使斜面体向右做匀速直线运动,通过的位移为x,物体相对斜面体一直保持静止,则在这个过程中( )| A. | 弹力对物体做功为Gxcosα | B. | 静摩擦力对物体做功为Gxsinα | ||
| C. | 重力对物体做功为Gx | D. | 合力对物体做功为0 |
1. 如图所示,质量为m的小物块放在粗糙水平圆盘上,随圆盘一起然圆心O以角速度ω匀速转动,若物块与圆盘间的动摩擦因数为μ,物块到转轴的距离为R,重力加速度为g,则物块所受摩擦力( )
如图所示,质量为m的小物块放在粗糙水平圆盘上,随圆盘一起然圆心O以角速度ω匀速转动,若物块与圆盘间的动摩擦因数为μ,物块到转轴的距离为R,重力加速度为g,则物块所受摩擦力( )
 如图所示,质量为m的小物块放在粗糙水平圆盘上,随圆盘一起然圆心O以角速度ω匀速转动,若物块与圆盘间的动摩擦因数为μ,物块到转轴的距离为R,重力加速度为g,则物块所受摩擦力( )
如图所示,质量为m的小物块放在粗糙水平圆盘上,随圆盘一起然圆心O以角速度ω匀速转动,若物块与圆盘间的动摩擦因数为μ,物块到转轴的距离为R,重力加速度为g,则物块所受摩擦力( )| A. | 大小一定等于mRω2 | B. | 大小一定等于μmg | ||
| C. | 方向指向圆心O | D. | 方向与物块运动的反向相反 |
3. 一件行李重为G,被绳OA和OB吊在空中,OA绳和OB绳的拉力分别为F1、F2,如图所示,则( )
一件行李重为G,被绳OA和OB吊在空中,OA绳和OB绳的拉力分别为F1、F2,如图所示,则( )
 一件行李重为G,被绳OA和OB吊在空中,OA绳和OB绳的拉力分别为F1、F2,如图所示,则( )
一件行李重为G,被绳OA和OB吊在空中,OA绳和OB绳的拉力分别为F1、F2,如图所示,则( )| A. | F1、F2的合力是G | |
| B. | F1、F2的合力是F | |
| C. | 行李对绳OA的拉力方向与F1方向相反,大小相等 | |
| D. | 行李受到重力G、OA绳的拉力F1、OB绳的拉力F2,还有F共四个力作用 |
4.一质点以速度v0做匀速直线运动,现对其施加一与v0方向垂直的恒力,且原来作用在质点上的力不发生改变,则( )
| A. | 质点将做平抛运动 | |
| B. | 质点将做匀速圆周运动 | |
| C. | 质点加速度的方向一定与该恒力的方向相同 | |
| D. | 质点相同时间内速度的变化量一定是相同的 |
 如图所示,细线下面悬挂一钢球(可看作质点),钢球在水平面内以O′为圆心做匀速圆周运动.若测得钢球做圆周运动的轨道半径为r,悬点O到圆心O′之间的距离为h,钢球质量为m.忽略空气阻力,重力加速度为g.求:
如图所示,细线下面悬挂一钢球(可看作质点),钢球在水平面内以O′为圆心做匀速圆周运动.若测得钢球做圆周运动的轨道半径为r,悬点O到圆心O′之间的距离为h,钢球质量为m.忽略空气阻力,重力加速度为g.求: 光滑水平面上,用轻质弹簧连接的质量为mA=2kg,mB=3kg的A、B两物体都处于静止状态,此时弹簧处于原长状态.将质量为mC=5kg的物体C,从半径为R=3.2m的$\frac{1}{4}$光滑圆周轨道最高点由静止释放,如图所示,圆周轨道的最低点与水平面相切,B与C碰撞后粘在一起运动,求:
光滑水平面上,用轻质弹簧连接的质量为mA=2kg,mB=3kg的A、B两物体都处于静止状态,此时弹簧处于原长状态.将质量为mC=5kg的物体C,从半径为R=3.2m的$\frac{1}{4}$光滑圆周轨道最高点由静止释放,如图所示,圆周轨道的最低点与水平面相切,B与C碰撞后粘在一起运动,求:


