题目内容
14. 竖直平面内光滑圆轨道外侧,一小球以某一水平速度v0从最高点A出发沿圆轨道运动,至B点时脱离轨道,最终落在水平面上的C点,不计空气阻力.下列说法中正确的是( )
竖直平面内光滑圆轨道外侧,一小球以某一水平速度v0从最高点A出发沿圆轨道运动,至B点时脱离轨道,最终落在水平面上的C点,不计空气阻力.下列说法中正确的是( )| A. | 在A点时,小球对圆轨道压力等于其重力 | |
| B. | 在B点时,小球的加速度方向指向圆心 | |
| C. | A到B过程中,小球水平方向的加速度先增大后减小 | |
| D. | A到C过程中,小球的机械能不守恒 |
分析 在A点受力分析,由牛顿第二定律与向心力公式可知,小球受到的支持力与重力的关系;由于A到B小球速度增加,则由${a}_{n}=m\frac{{v}^{2}}{r}$,可知向心加速度的大小变化,从A到C过程中,小球只有重力做功,小球的机械能守恒.
解答 解:A、小球在A点时,根据牛顿第二定律得:$mg-N=m\frac{{v}^{2}}{r}$,可得:小球受到的支持力小于其重力,即小球对圆轨道压力小于其重力,故A错误.
B、小球在B点刚离开轨道,则小球对圆轨道的压力为零,只受重力作用,加速度竖直向下,故B错误.
C、小球在A点时合力沿竖直方向,在B点时合力也沿竖直方向,但在中间过程某点支持力却有水平向右的分力,所以小球水平方向的加速度必定先增加后减小,故C正确.
D、从A到C过程中,小球只有重力做功,小球的机械能守恒.故D错误.
故选:C
点评 考查竖直平面内的变速圆周运动与斜抛运动,涉及牛顿第二定律,向心力公式,向心加速度表达式.注意变速圆周运动速度方向不但变化,而且大小也发生变化.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
4.地月系统中,若忽略其它天体的影响,可将地球和月球看成双星系统,即地球和月球在彼此引力作用下做匀速圆周运动.假如人类对地球的污染越来越严重,导致地球不适合人类居住,人类携带物资逐渐向月球进驻.假设经过长时间迁移后,地球和月球仍可以看作均匀球体,地球和月球之间的距离保持不变,则( )
| A. | 地球与月球之间的引力增大 | B. | 地球与月球之间的引力减小 | ||
| C. | 月球运动的周期不变 | D. | 月球运动的周期减小 |
2.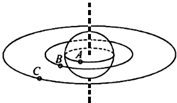 我国在2015年年底发射首颗地球同步轨道高分辨率对地观测卫星高分四号.如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )
我国在2015年年底发射首颗地球同步轨道高分辨率对地观测卫星高分四号.如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )
 我国在2015年年底发射首颗地球同步轨道高分辨率对地观测卫星高分四号.如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )
我国在2015年年底发射首颗地球同步轨道高分辨率对地观测卫星高分四号.如图所示,A是静止在赤道上随地球自转的物体,B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列判断正确的是( )| A. | 卫星B的线速度大于卫星C的线速度 | |
| B. | 物体A随地球自转的周期大于卫星C的周期 | |
| C. | 物体A随地球自转的加速度大于卫星C的加速度 | |
| D. | 物体A随地球自转的角速度大于卫星B的角速度 |
9.以下四幅图对应着四个重要的实验.下列说法中正确的是( )
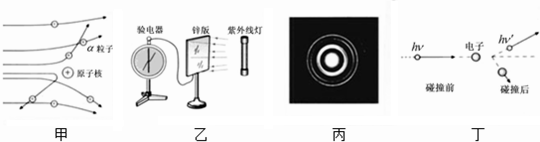

| A. | 甲图和丙图对应的实验,说明了原子内部是非常空旷的,并可以据此估算出原子核的大小 | |
| B. | 通过乙图和丁图对应的实验,用碰撞模型对实验现象做出了解释,使认识到光子具有能量和动量,说明光具有粒子性 | |
| C. | 通过乙图对应的实验,提出光子说,但在认为光有粒子性的同时,并没有否定光的波动性,因为光子的能量E=hν,其中ν为光的频率--这是描述波的物理量之一 | |
| D. | 通过丙图对应的实验,发现电子具有波动性,其波长和动量的关系为λ=hp |
19.如图所示是原子核的核子平均质量与原子序数Z的关系图象,下列说法正确的是( )


| A. | 若DE能结合成F,结合过程一定能放出核能 | |
| B. | 若DE能结合成F,结合过程一定要吸收能量 | |
| C. | 若CB能结合成A,结合过程一定要放出能量 | |
| D. | 若CB能结合成A,结合过程一定要吸收能量 |
8.哈雷彗星绕太阳运动的轨道是比较扁的椭圆.下面说法中正确的是( )
| A. | 彗星在近日点的速率大于在远日点的速率 | |
| B. | 彗星在近日点的向心加速度大于在远日点的向心加速度 | |
| C. | 若彗星的周期为75年,则它的半长轴是地球公转半径的75倍 | |
| D. | 彗星在近日点的角速度大于在远日点的角速度 |
 如图所示,AB为倾角θ=37°的粗糙斜面轨道,通过一小段光滑圆弧与光滑水平轨道BC相连接,质量为m乙的小球乙静止在水平轨道上,质量为m甲的小球甲以速度v0与乙球发生弹性正碰.若m甲:m乙=2:3,且轨道足够长.sin37°=0.6,cos37°=0.8.求:
如图所示,AB为倾角θ=37°的粗糙斜面轨道,通过一小段光滑圆弧与光滑水平轨道BC相连接,质量为m乙的小球乙静止在水平轨道上,质量为m甲的小球甲以速度v0与乙球发生弹性正碰.若m甲:m乙=2:3,且轨道足够长.sin37°=0.6,cos37°=0.8.求: