题目内容
19. 如图甲,光滑的水平面上有三个滑块a、b、c;ma=1kg,mb=3kg;b、c被一根轻质弹簧连接在一起,处于静止状态;在t=0时,滑块a突然以水平向右的速度与b正碰,并瞬间粘合成一个物体(记为d);此后运动过程中弹簧始终处于弹性限度内,d的速度随时间做周期性变化,如图乙.则:
如图甲,光滑的水平面上有三个滑块a、b、c;ma=1kg,mb=3kg;b、c被一根轻质弹簧连接在一起,处于静止状态;在t=0时,滑块a突然以水平向右的速度与b正碰,并瞬间粘合成一个物体(记为d);此后运动过程中弹簧始终处于弹性限度内,d的速度随时间做周期性变化,如图乙.则:①求滑块a的初速度大小以及a、b正碰中损失的机械能△E;
②求滑块c的质量.
分析 由图乙所示图象求出速度,分析清楚过程,应用动量守恒定律与能量守恒定律分析答题.
解答 解:(1)由图乙所示图象可知,a、b粘合后瞬间的速度大小:vd1=1m/s…①,
a、b正碰过程中动量守恒,以a的初速度方向为正方向,由动量守恒定律得:mav0=mdvd1…②,
解得,滑块a的初速度:v0=4m/s…③,
由能量守恒定律可得a、b正碰中损失的机械能:△E=$\frac{1}{2}$mav02-$\frac{1}{2}$mdvd12…④
代入数据解得:△E=6J;
(2)由图乙所示可知,弹簧第一次恢复形变瞬间,d的速度为:vd2=-0.5m/s…⑤
d、c和弹簧构成的系统动量守恒、机械能守恒,以d、c系统的初速度方向为正方向,由动量守恒定律得:
mdvd1=mdvd2+mcvc2…⑥
由能量守恒定律得:$\frac{1}{2}{m}_{d}{v}_{d1}^{2}=\frac{1}{2}{m}_{d}{v}_{d2}^{2}+\frac{1}{2}{m}_{c}{v}_{c2}^{2}$…⑦
代入数据解得滑块c的质量为:mc=12kg…⑧;
答:(1)滑块a的初速度大小为4m/s,a、b正碰中损失的机械能△E为6J;
(2)滑块c的质量为12kg;
点评 本题考查了动量守恒定律的应用,本题物体运动过程复杂、分析清楚物体运动过程是正确解题的前提与关键,由图示图象求出物体的速度、应用动量守恒定律与能量守恒定律即可正确解题.

练习册系列答案
相关题目
10.如图甲所示,在杂技表演中,猴子沿竖直杆向上运动,其v-t图象如图乙所示,人顶杆沿水平地面运动的x-t图象如图丙所示.若以地面为参考系,下列说法正确的是( )


| A. | 猴子的运动轨迹为直线 | |
| B. | 猴子在2 s内做匀变速曲线运动 | |
| C. | t=0时猴子的速度大小为8 m/s | |
| D. | t=2 s时猴子的加速度大小为2 m/s2 |
14. 如图甲为理想变压器,其原、副线圈的匝数比为4:1,原线圈接图乙所示的正弦交流电.图中RT为阻值随温度升高而减小的热敏电阻,R1为定值电阻,电压表和电流表均为理想电表.则下列说法正确的是( )
如图甲为理想变压器,其原、副线圈的匝数比为4:1,原线圈接图乙所示的正弦交流电.图中RT为阻值随温度升高而减小的热敏电阻,R1为定值电阻,电压表和电流表均为理想电表.则下列说法正确的是( )
 如图甲为理想变压器,其原、副线圈的匝数比为4:1,原线圈接图乙所示的正弦交流电.图中RT为阻值随温度升高而减小的热敏电阻,R1为定值电阻,电压表和电流表均为理想电表.则下列说法正确的是( )
如图甲为理想变压器,其原、副线圈的匝数比为4:1,原线圈接图乙所示的正弦交流电.图中RT为阻值随温度升高而减小的热敏电阻,R1为定值电阻,电压表和电流表均为理想电表.则下列说法正确的是( )| A. | 图乙所示电压的瞬时值表达式为u=51sin50πt(V) | |
| B. | 变压器原、副线圈中的电流、频率之比为1:4 | |
| C. | 变压器输入、输出功率之比为1:1 | |
| D. | RT处温度升高时,电压表和电流表的示数均变大 |
4. 两个横截面分别为圆和正方形,磁感应强度相同的匀强磁场,圆的直径和正方形的边长相等,两个电子分别以相同的速度同时飞入两个磁场区域,速度方向均与磁场方向垂直,进入圆形磁场的电子初速度方向对准圆心;进入正方形磁场的电子初速度方向垂直于边界,从中点进入.则下面判断正确的是( )
两个横截面分别为圆和正方形,磁感应强度相同的匀强磁场,圆的直径和正方形的边长相等,两个电子分别以相同的速度同时飞入两个磁场区域,速度方向均与磁场方向垂直,进入圆形磁场的电子初速度方向对准圆心;进入正方形磁场的电子初速度方向垂直于边界,从中点进入.则下面判断正确的是( )
 两个横截面分别为圆和正方形,磁感应强度相同的匀强磁场,圆的直径和正方形的边长相等,两个电子分别以相同的速度同时飞入两个磁场区域,速度方向均与磁场方向垂直,进入圆形磁场的电子初速度方向对准圆心;进入正方形磁场的电子初速度方向垂直于边界,从中点进入.则下面判断正确的是( )
两个横截面分别为圆和正方形,磁感应强度相同的匀强磁场,圆的直径和正方形的边长相等,两个电子分别以相同的速度同时飞入两个磁场区域,速度方向均与磁场方向垂直,进入圆形磁场的电子初速度方向对准圆心;进入正方形磁场的电子初速度方向垂直于边界,从中点进入.则下面判断正确的是( )| A. | 两电子在磁场中运动的时间有可能相同 | |
| B. | 两电子在两磁场中运动时,其半径可能不相同 | |
| C. | 进入圆形磁场区域的电子可能先飞离磁场 | |
| D. | 进入圆形磁场区域的电子可能后飞离磁场 |
11. 如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A点以速度v0水平抛出,不计空气阻力.则下列判断正确的是( )
如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A点以速度v0水平抛出,不计空气阻力.则下列判断正确的是( )
 如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A点以速度v0水平抛出,不计空气阻力.则下列判断正确的是( )
如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A点以速度v0水平抛出,不计空气阻力.则下列判断正确的是( )| A. | 若v0取值不同,初速度大的小球运动时间长 | |
| B. | 小球落到半圆形轨道的瞬间,速度方向沿半径方向 | |
| C. | 要使小球掉到环上时的竖直分速度最大,小球应该落在BC之间 | |
| D. | 无论v0取何值,小球都不可能垂直撞击半圆环 |
8.一定质量的理想气体,状态变化过程如V-T图象中ABC图线所示,由图线可知( )


| A. | A→B过程,气体吸热、压强增大 | |
| B. | B→C过程,气体放热、压强增大 | |
| C. | C→A过程,分子密度减小 | |
| D. | C→A过程,分子在单位时间内撞击单位面积容器壁的次数增加 |
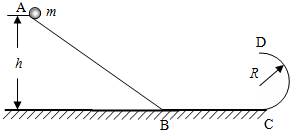 如图所示,斜面AB、水平轨道BC和半圆形轨道CD平滑连接,AB、BC和CD处于同一平面内,CD的半径为R=0.4m.质量m=0.5kg的小球(可看做质点)从A点静止开始下滑,恰能到达D点.不计一切摩擦,g取10m/s2,求:
如图所示,斜面AB、水平轨道BC和半圆形轨道CD平滑连接,AB、BC和CD处于同一平面内,CD的半径为R=0.4m.质量m=0.5kg的小球(可看做质点)从A点静止开始下滑,恰能到达D点.不计一切摩擦,g取10m/s2,求: 如图所示,长l=1.25m,质量M=8kg的平板车静止在光滑水平面上,车的左端放一质量m=2kg的木块,它与车面间的动摩擦因数μ=0.2,今以水平恒力F=10N拖木板在车上滑行,物体最终从车的右端滑落,木块在小车上滑动的过程中,问:
如图所示,长l=1.25m,质量M=8kg的平板车静止在光滑水平面上,车的左端放一质量m=2kg的木块,它与车面间的动摩擦因数μ=0.2,今以水平恒力F=10N拖木板在车上滑行,物体最终从车的右端滑落,木块在小车上滑动的过程中,问: