题目内容
4. 如图所示,劲度系数分别为K1和K2的两根弹簧,K1>K2,质量m1,m2的两个小物块,且m1>m2,现要求两根弹簧的总长最短,则应使( )
如图所示,劲度系数分别为K1和K2的两根弹簧,K1>K2,质量m1,m2的两个小物块,且m1>m2,现要求两根弹簧的总长最短,则应使( )| A. | K1在上,m1在上 | B. | K1在上,m2在上 | C. | K2在上,m1在上 | D. | K2在上,m2在上 |
分析 弹簧和物体共有四种组合方式,分别对上下两个物体受力分析,然后结合胡克定律求解出弹簧的总长度.
解答 解:把物体压在弹簧的上端,物体静止处于平衡状态,弹簧的弹力F等于物体的重力G,即F=G.
由胡克定律F=kx知,在力F一定时,k越小弹簧的伸长量x越大.对于下面的弹簧来说它的弹力F下=(m1+m2)g=kx下,
由于(m1+m2)g一定,要使x下小一些,k应大,已知k1>k2,所以k1应在下面,k2在上面.由胡克定律F=kx知,在k一定时,F越小弹簧的伸长量x越小,要使x小,已知m1>m2,所以m1应在k2上面,所以k1在下,m1在上,两根弹簧的总长度最短.
故C正确、ABD错误;
故选C.
点评 此题考查了胡克定律的应用,要记住胡克定律公式F=kx及各符号表示什么量.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
14. 环形对撞机是研究高能粒子的重要装置,如图所示正、负粒子由静止经过电压为U的直线加速器加速后,沿圆环切线方向注入对撞机的真空环状空腔内,空腔内存在与圆环平面垂直的匀强磁场,调节磁感应强度的大小可使两种带电粒子被局限在环状空腔内,沿相反方向做半径相等的匀速圆周运动,并在碰撞区内迎面相撞.为维持带电粒子沿环状空腔的中心线做匀速圆周运动,下列说法正确是( )
环形对撞机是研究高能粒子的重要装置,如图所示正、负粒子由静止经过电压为U的直线加速器加速后,沿圆环切线方向注入对撞机的真空环状空腔内,空腔内存在与圆环平面垂直的匀强磁场,调节磁感应强度的大小可使两种带电粒子被局限在环状空腔内,沿相反方向做半径相等的匀速圆周运动,并在碰撞区内迎面相撞.为维持带电粒子沿环状空腔的中心线做匀速圆周运动,下列说法正确是( )
 环形对撞机是研究高能粒子的重要装置,如图所示正、负粒子由静止经过电压为U的直线加速器加速后,沿圆环切线方向注入对撞机的真空环状空腔内,空腔内存在与圆环平面垂直的匀强磁场,调节磁感应强度的大小可使两种带电粒子被局限在环状空腔内,沿相反方向做半径相等的匀速圆周运动,并在碰撞区内迎面相撞.为维持带电粒子沿环状空腔的中心线做匀速圆周运动,下列说法正确是( )
环形对撞机是研究高能粒子的重要装置,如图所示正、负粒子由静止经过电压为U的直线加速器加速后,沿圆环切线方向注入对撞机的真空环状空腔内,空腔内存在与圆环平面垂直的匀强磁场,调节磁感应强度的大小可使两种带电粒子被局限在环状空腔内,沿相反方向做半径相等的匀速圆周运动,并在碰撞区内迎面相撞.为维持带电粒子沿环状空腔的中心线做匀速圆周运动,下列说法正确是( )| A. | 对于给定的加速电压,带电粒子的比荷$\frac{q}{m}$越大,磁感应强度B越小 | |
| B. | 对于给定的加速电压,带电粒子的比荷$\frac{q}{m}$越大,磁感应强度B越大 | |
| C. | 对于给定的带电粒子,加速电压U越大,粒子做圆周运动的周期越大 | |
| D. | 对于给定的带电粒子,粒子做圆周运动的周期与加速电压U无关 |
15. 如图所示,间距为l的两平行光滑金属导轨倾斜放置,匀强磁场垂直于导轨平面向上,将质量为m的导体棒放在导轨上,导体棒与导轨垂直且接触良好.当导体棒中通有从P到Q、大小为I的电流时,棒的加速度大小为a1;现将电流反向,其它条件不变,棒的加速度大小变为a2,若a1、a2均沿斜面向下,则该磁场的磁感应强度大小可表示为( )
如图所示,间距为l的两平行光滑金属导轨倾斜放置,匀强磁场垂直于导轨平面向上,将质量为m的导体棒放在导轨上,导体棒与导轨垂直且接触良好.当导体棒中通有从P到Q、大小为I的电流时,棒的加速度大小为a1;现将电流反向,其它条件不变,棒的加速度大小变为a2,若a1、a2均沿斜面向下,则该磁场的磁感应强度大小可表示为( )
 如图所示,间距为l的两平行光滑金属导轨倾斜放置,匀强磁场垂直于导轨平面向上,将质量为m的导体棒放在导轨上,导体棒与导轨垂直且接触良好.当导体棒中通有从P到Q、大小为I的电流时,棒的加速度大小为a1;现将电流反向,其它条件不变,棒的加速度大小变为a2,若a1、a2均沿斜面向下,则该磁场的磁感应强度大小可表示为( )
如图所示,间距为l的两平行光滑金属导轨倾斜放置,匀强磁场垂直于导轨平面向上,将质量为m的导体棒放在导轨上,导体棒与导轨垂直且接触良好.当导体棒中通有从P到Q、大小为I的电流时,棒的加速度大小为a1;现将电流反向,其它条件不变,棒的加速度大小变为a2,若a1、a2均沿斜面向下,则该磁场的磁感应强度大小可表示为( )| A. | $\frac{{m(a}_{1}{+}_{{a}_{2}})}{2IL}$ | B. | $\frac{{m(a}_{1}{-}_{{a}_{2}})}{2IL}$ | C. | $\frac{{m(a}_{1}{+}_{{a}_{2}})}{IL}$ | D. | $\frac{{m(a}_{2}{-}_{{a}_{1}})}{2IL}$ |
9. 如图所示,光滑的小圆弧轨道半径为r,光滑的大圆弧轨道半径为4r,小球质量为m(可视为质点),小圆弧与大圆弧的圆心O1、O2在同一竖线上,两圆弧的最低点重合,两圆弧轨道固定在同一竖直平面内.小球从大圆弧轨道上与O2等高处由静止释放,小球通过小圆弧轨道最高点时对轨道的压力的大小为( )
如图所示,光滑的小圆弧轨道半径为r,光滑的大圆弧轨道半径为4r,小球质量为m(可视为质点),小圆弧与大圆弧的圆心O1、O2在同一竖线上,两圆弧的最低点重合,两圆弧轨道固定在同一竖直平面内.小球从大圆弧轨道上与O2等高处由静止释放,小球通过小圆弧轨道最高点时对轨道的压力的大小为( )
 如图所示,光滑的小圆弧轨道半径为r,光滑的大圆弧轨道半径为4r,小球质量为m(可视为质点),小圆弧与大圆弧的圆心O1、O2在同一竖线上,两圆弧的最低点重合,两圆弧轨道固定在同一竖直平面内.小球从大圆弧轨道上与O2等高处由静止释放,小球通过小圆弧轨道最高点时对轨道的压力的大小为( )
如图所示,光滑的小圆弧轨道半径为r,光滑的大圆弧轨道半径为4r,小球质量为m(可视为质点),小圆弧与大圆弧的圆心O1、O2在同一竖线上,两圆弧的最低点重合,两圆弧轨道固定在同一竖直平面内.小球从大圆弧轨道上与O2等高处由静止释放,小球通过小圆弧轨道最高点时对轨道的压力的大小为( )| A. | 2mg | B. | 3mg | C. | 4mg | D. | 5mg |
16. 空间存在一沿x轴方向的静电场,以x正方向为电场强度的正方向,电场强度E随x变化的关系如图所示,图线关于坐标原点对称,A、B是x轴上关于原点对称的两点,下列说法中不正确的是( )
空间存在一沿x轴方向的静电场,以x正方向为电场强度的正方向,电场强度E随x变化的关系如图所示,图线关于坐标原点对称,A、B是x轴上关于原点对称的两点,下列说法中不正确的是( )
 空间存在一沿x轴方向的静电场,以x正方向为电场强度的正方向,电场强度E随x变化的关系如图所示,图线关于坐标原点对称,A、B是x轴上关于原点对称的两点,下列说法中不正确的是( )
空间存在一沿x轴方向的静电场,以x正方向为电场强度的正方向,电场强度E随x变化的关系如图所示,图线关于坐标原点对称,A、B是x轴上关于原点对称的两点,下列说法中不正确的是( )| A. | 电子在A、B两点的电势能相等 | |
| B. | 电子在A、B两点的加速度方向相反 | |
| C. | 取无穷远处电势为零,则O点处电势亦为零 | |
| D. | 电子从A点由静止释放后的运动轨迹可能是曲线 |
16.极板间距为d的平行板电容器,充电后与电源断开,一个动能为Ek的带电粒子,垂直于电场线方向飞入平行板电容器,飞出电容器时动能为2Ek,如果使这个带电粒子的初动能变为原来的两倍,同时将电容器极板间距变为d′=$\frac{d}{2}$,则它飞出电容器时的动能变为( )
| A. | 4Ek | B. | 3.5Ek | C. | 3Ek | D. | 2.5Ek |
17. 如图为蹦床比赛某运动员从高处下落到蹦床后又被弹回原高度过程中的速度随时间变化的图象,0~t1时段和t7~t8间段图线为直线,若时0~t8时间内相邻时刻时间间隔相等,则( )
如图为蹦床比赛某运动员从高处下落到蹦床后又被弹回原高度过程中的速度随时间变化的图象,0~t1时段和t7~t8间段图线为直线,若时0~t8时间内相邻时刻时间间隔相等,则( )
 如图为蹦床比赛某运动员从高处下落到蹦床后又被弹回原高度过程中的速度随时间变化的图象,0~t1时段和t7~t8间段图线为直线,若时0~t8时间内相邻时刻时间间隔相等,则( )
如图为蹦床比赛某运动员从高处下落到蹦床后又被弹回原高度过程中的速度随时间变化的图象,0~t1时段和t7~t8间段图线为直线,若时0~t8时间内相邻时刻时间间隔相等,则( )| A. | t3、t5时刻运动员处于失重状态 | |
| B. | t6时刻运动员重力势能最小,蹦床弹性势能最大 | |
| C. | t2时刻运动员受力平衡,运动员动能最大 | |
| D. | t1、t7时刻运动员速度相同 |
 如图所示,无限大均匀带正电薄板竖直放置,其周围空间的电场可认为是匀强电场.光滑绝缘细管垂直于板穿过中间小孔,一个视为质点的带负电小球在细管内运动(细管绝缘且光滑).以小孔为原点建立x轴,规定x轴正方向为加速度a、速度v的正方向,如图分别表示x轴上各点的电势φ,小球的加速度a、速度v和动能Ek随x的变化图象,其中正确的是( )
如图所示,无限大均匀带正电薄板竖直放置,其周围空间的电场可认为是匀强电场.光滑绝缘细管垂直于板穿过中间小孔,一个视为质点的带负电小球在细管内运动(细管绝缘且光滑).以小孔为原点建立x轴,规定x轴正方向为加速度a、速度v的正方向,如图分别表示x轴上各点的电势φ,小球的加速度a、速度v和动能Ek随x的变化图象,其中正确的是( )



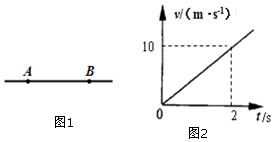 如图,A、B是-条电场线上的两点,t=0时刻从A点释放一初速为零的电子,电子仅在电场力作用下,沿直线从A运动到B,其速度随时间变化的规律如图所示.t=2s时到达B点速度大小为10m/s.已知电子质量为m,电荷量大小为e.求:
如图,A、B是-条电场线上的两点,t=0时刻从A点释放一初速为零的电子,电子仅在电场力作用下,沿直线从A运动到B,其速度随时间变化的规律如图所示.t=2s时到达B点速度大小为10m/s.已知电子质量为m,电荷量大小为e.求: