题目内容
19. 如图所示,质量m的小物体,从光滑的$\frac{1}{4}$圆弧轨道上与圆心等高处由静止释放,到达底端时进入总长为L的水平传送带,传送带可由一电机驱使顺时针转动.已知物体与传送带间的动摩擦因数为μ,$\frac{1}{4}$圆弧轨道半径为r.求:
如图所示,质量m的小物体,从光滑的$\frac{1}{4}$圆弧轨道上与圆心等高处由静止释放,到达底端时进入总长为L的水平传送带,传送带可由一电机驱使顺时针转动.已知物体与传送带间的动摩擦因数为μ,$\frac{1}{4}$圆弧轨道半径为r.求:(1)求物体刚到达轨道底端时速度v0及对轨道压力的大小;
(2)若电机不开启,传送带不动,物体能够从传送带右端滑出,则物体到达传送带右端时的速度;
(3)若开启电机,传送带以速率v2顺时针转动.已知物体在传送带上能加速,且到达传送带右端前速度已达到v2,则传送一个物体电动机对传送带多做的功为多少?
分析 (1)物体在曲面上运动时,机械能守恒,根据机械能守恒定律求出物体到达曲面底端时的速度大小.由牛顿运动定律求物体对轨道的压力.
(2)对在传送带上的运动过程,运用动能定理,求出物体滑离传送带右端时的速度大小.
(3)根据牛顿第二定律求出物体在传送带上运行的加速度,结合速度时间公式求出运行的时间,从而得出这段过程中传送带的位移,根据能量守恒得出传送一个物体电动机多做的功.
解答 解:(1)物体滑下过程机械能守恒,有:$mgr=\frac{1}{2}mv_0^2$ 得 ${v_0}=\sqrt{2gr}$
根据牛顿第二定律:$N-mg=m\frac{v_0^2}{r}$
可得 N=3mg
根据牛顿第三定律,物体对轨道压力 N′=N=3mg
(2)从物体开始下落到它到达传送带右端,根据动能定理得
$mgr-μmgL=\frac{1}{2}mv_1^2$
则 ${v_1}=\sqrt{2g(r-μL)}$
(3)物体先加速后匀速,匀速阶段没有摩擦力,不再对物体做功
加速阶段多做的功为传送带克服摩擦力做的功 W=μmg•s带
传送带位移 s带=v2t
加速时间 $t=\frac{{{v_2}-{v_0}}}{μg}$
解得 $W=m{v_2}({v_2}-{v_0})=m{v_2}({v_2}-\sqrt{2gr})$
(或用 $W=Q+\frac{1}{2}mv_2^2-\frac{1}{2}mv_0^2$,摩擦生热 Q=μmg(s带-s物),物体位移s物=$\frac{{v}_{2}^{2}-{v}_{0}^{2}}{2μg}$求解)
答:
(1)物体刚到达轨道底端时速度v0为$\sqrt{2gr}$,对轨道压力的大小为3mg.
(2)物体到达传送带右端时的速度为$\sqrt{2g(r-μL)}$.
(3)传送一个物体电动机对传送带多做的功为mv2(v2-$\sqrt{2gr}$).
点评 本题综合考查了机械能守恒定律、动能定理和能量守恒定律,要知道电动机多做的功等于摩擦力对传送带做功的大小.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | 已知该卫星的质量是1.24t,若它的质量增加到2.48t,则其同步轨道半径变为原来的2倍 | |
| B. | 它的运行速度一定小于7.9km/s | |
| C. | 它可以经过北京的正上空,所以我国利用它进行电视转播 | |
| D. | 它距离地面的高度约为地球半径的5.6倍,所以它的向心加速度约为其下方地面上的物体重力加速度的$\frac{1}{5.6}$ |
| A. | 物体在水平面上匀速运动,合力所做的功 | |
| B. | 物体在水平面上匀速运动,支持力所做的功 | |
| C. | 物体自由下落,重力所做的功 | |
| D. | 物体做匀速圆周运动,合力所做的功 |
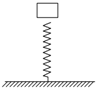 如图所示,地面上竖直放一根轻弹簧,其下端和地面连接,一物体从弹簧正上方距弹簧一定高度处自由下落,则( )
如图所示,地面上竖直放一根轻弹簧,其下端和地面连接,一物体从弹簧正上方距弹簧一定高度处自由下落,则( )| A. | 物体和弹簧接触时,物体的动能最大 | |
| B. | 物体在反弹阶段,动能一直增加,直到物体脱离弹簧为止 | |
| C. | 与弹簧接触的整个过程,物体的动能与重力势能之和先增大后减小 | |
| D. | 与弹簧接触的整个过程,物体的动能与弹簧弹性势能之和先增大后减小 |
 如图所示,质量为m的物体A静止在倾角为θ=30°、质量为M的斜面体B上.现用水平力F推物体A,在F由零增大至$\frac{\sqrt{3}mg}{2}$再逐渐减为零的过程中,A和B始终保持静止.对此过程下列说法正确的是( )
如图所示,质量为m的物体A静止在倾角为θ=30°、质量为M的斜面体B上.现用水平力F推物体A,在F由零增大至$\frac{\sqrt{3}mg}{2}$再逐渐减为零的过程中,A和B始终保持静止.对此过程下列说法正确的是( )| A. | 地面对B的支持力大于(M+m)g | |
| B. | A对B的压力的最小值为$\frac{\sqrt{3}mg}{2}$,最大值为$\frac{3\sqrt{3}mg}{4}$ | |
| C. | A受到摩擦力的最小值为0,最大值为$\frac{mg}{4}$ | |
| D. | A受到摩擦力的最小值为$\frac{mg}{2}$,最大值为$\frac{3mg}{4}$ |

| A. | 甲图是卡文迪许测定引力常量的实验 | |
| B. | 乙图中玻璃管抽成真空后,重的物体比轻的物体下落的快 | |
| C. | 丙图中砝码所受到的重力等于小车的合外力 | |
| D. | 丁图是伽利略说明“力不是维持物体运动状态的原因”所用的实验装置 |
 某兴趣小组对一辆自制遥控小车的性能进行研究.他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段图象为曲线外,其余时间段图象均为直线).已知在小车运动的过程中,小车的额定功率P=9W,小车的质量为1.0kg,可认为在整个运动过程中小车所受到的阻力大小不变.求:
某兴趣小组对一辆自制遥控小车的性能进行研究.他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段图象为曲线外,其余时间段图象均为直线).已知在小车运动的过程中,小车的额定功率P=9W,小车的质量为1.0kg,可认为在整个运动过程中小车所受到的阻力大小不变.求: 如图所示的系统,绳子的质量忽略不计且绳子不可以伸长,滑轮和绳子的摩擦力忽略不计,求M1的加速度.
如图所示的系统,绳子的质量忽略不计且绳子不可以伸长,滑轮和绳子的摩擦力忽略不计,求M1的加速度.