题目内容
13.如图所示,两光滑斜面与光滑水平面间夹角均为θ,两斜面末端与水平面平滑对接.可视为质点的物块A、B质量分别为m、βm(β为待定系数),物块A从左边斜面h高处由静止开始沿斜面下滑,与静止于水平轨道的物块B正面相撞,碰后物块A、B立即分开,它们能达到的最大高度均为$\frac{1}{4}$h.两物块经过斜面与水平面连接处及碰撞过程中均没有机械能损失,重力加速度为g.求:
(1)待定系数β;
(2)第一次碰撞刚结束时木块A、B各自的速度;
(3)物块A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论木块A、B在轨道最低处第n次碰撞刚结束时各自的速度.
分析 (1)由机械能守恒即可求出待定系数β;
(2)由于没有机械能的损失,可知在碰撞的过程中动量守恒与机械能守恒,由此即可求出第一次碰撞刚结束时木块A、B各自的速度;
(3)结合机械能守恒与动量守恒即可求出第二次碰撞后的速度,然后由归纳法得出在轨道最低处第n次碰撞刚结束时各自的速度.
解答 解:(1)碰撞过程中均没有机械能损失,由机械能守恒得:$mgh=\frac{mgh}{4}+\frac{βmgh}{4}$
得 β=3
(2)A到达最低点的速度:${v}_{0}=\sqrt{2gh}$
设 A、B 碰撞后的速度分别为 v1、v2,设向右为正、向左为负,则
$\frac{1}{2}βm{v_2}^2=\frac{βmgh}{4}$
mv0=mv1+βmv2
联立得:${v_1}=-\sqrt{\frac{1}{2}gh}$,方向向左${v_2}=\sqrt{\frac{1}{2}gh}$,方向向右
(3)规定向右为正方向,设 A、B 第二次碰撞刚结束时的速度分别为 V1、V2,则
$\left\{\begin{array}{l}m{v_1}-βm{v_2}=m{V_1}+βm{V_2}\\ mgh=\frac{1}{2}m{V_1}^2+\frac{1}{2}βm{V_2}^2\end{array}\right.$
解得${V_1}=-\sqrt{2gh},{V_2}=0$(另一组解:V1=-v1,V2=-v2 不合题意,舍去)
由此可得:
当 n为奇数时,小球 A、B 在第 n次碰撞刚结束时的速度分别与其第一次碰撞刚结束时相同;
当 n为偶数时,小球 A、B 在第 n次碰撞刚结束时的速度分别与其第二次碰撞刚结束时相同.
答:(1)待定系数β是3;
(2)第一次碰撞刚结束时木块A、B各自的速度是$-\sqrt{\frac{1}{2}gh}$和$\sqrt{\frac{1}{2}gh}$;
(3)物块A、B在轨道最低处第二次碰撞刚结束时各自的速度分别是$-\sqrt{2gh}$和0,论木块A、B在轨道最低处第n次碰撞刚结束时:当 n为奇数时,小球 A、B 在第 n次碰撞刚结束时的速度分别与其第一次碰撞刚结束时相同;当 n为偶数时,小球 A、B 在第 n次碰撞刚结束时的速度分别与其第二次碰撞刚结束时相同.
点评 该题的前两问比较简单,分别由动量守恒与能量守恒即可求出,解答的关键是第三问,要注意碰撞后的速度的方向与大小要合理.

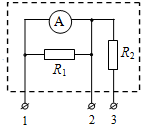 如图所示,其中电流表A的量程为0.6A,表盘均匀划分为30个小格,每一小格表示0.02A;R1的阻值等于电流表内阻的$\frac{1}{2}$;R2的阻值等于电流表内阻的2倍.若用电流表A的表盘刻度表示流过接线柱1的电流值,则下列分析正确的是( )
如图所示,其中电流表A的量程为0.6A,表盘均匀划分为30个小格,每一小格表示0.02A;R1的阻值等于电流表内阻的$\frac{1}{2}$;R2的阻值等于电流表内阻的2倍.若用电流表A的表盘刻度表示流过接线柱1的电流值,则下列分析正确的是( )| A. | 将接线柱1、2接入电路时,每一小格表示0.06A | |
| B. | 将接线柱1、2接入电路时,每一小格表示0.02A | |
| C. | 将接线柱1、3接入电路时,每一小格表示0.06A | |
| D. | 将接线柱1、3接入电路时,每一小格表示0.01A |
| A. | 一定质量的气体膨胀对外做功l00J,同时从外界吸收120J的热量,则它的内能增加大20J | |
| B. | 在使两个分子间的距离由很远(r>10-9m)减小到很难再靠近的过程中先减小后增大,分子势能不断增大 | |
| C. | 由于液体表面层分子间距离大于液体内部分子问距离,液体表面存在张力 | |
| D. | 电冰箱的工作过程表明,热量可以从低温物体向高温物体传递 | |
| E. | 热量不能从低温物体传到高温物体 |
| A. | 扩散现象可以在液体和气体中进行,不能在固体中进行 | |
| B. | 当分子力表现为斥力时,分子势能随分子间距离的减小而增大 | |
| C. | 单晶体冰糖磨碎后熔点不会发生变化 | |
| D. | 外界对气体做功,气体的内能一定增加 | |
| E. | 自然发生的热传递过程是沿着分子热运动无序性增大的方向进行的 |
 如图所示,直杆BC的一端用铰链固定于竖直墙壁,另一端固定一个小滑轮C,细绳下端挂一重物,细绳的AC段水平.不计直杆、滑轮及细绳的质量,忽略所有摩擦.若将细绳的端点A稍向下移至A′点,使之重新平衡,则此时滑轮C的位置( )
如图所示,直杆BC的一端用铰链固定于竖直墙壁,另一端固定一个小滑轮C,细绳下端挂一重物,细绳的AC段水平.不计直杆、滑轮及细绳的质量,忽略所有摩擦.若将细绳的端点A稍向下移至A′点,使之重新平衡,则此时滑轮C的位置( )| A. | 在AA′之间 | B. | 与A′点等高 | C. | 在A′点之下 | D. | 在A点之上 |
| A. | 150W | B. | 300W | C. | 450W | D. | 600W |

 如图所示,质量为3kg的小车A以v0=4m/s的速度沿光滑水平面匀速运动,小车左端固定的支架通过不可伸长的轻绳悬挂质量为1kg的小球B(可看作质点),小球距离车面0.8m.某一时刻,小车与静止在水平面上的质量为1kg的物块C发生碰撞并粘连在一起(碰撞时间可忽略),此时轻绳突然断裂.此后,小球刚好落入小车右端固定的砂桶中(小桶的尺寸可忽略),不计空气阻力,重力加速度g取10m/s2.求:
如图所示,质量为3kg的小车A以v0=4m/s的速度沿光滑水平面匀速运动,小车左端固定的支架通过不可伸长的轻绳悬挂质量为1kg的小球B(可看作质点),小球距离车面0.8m.某一时刻,小车与静止在水平面上的质量为1kg的物块C发生碰撞并粘连在一起(碰撞时间可忽略),此时轻绳突然断裂.此后,小球刚好落入小车右端固定的砂桶中(小桶的尺寸可忽略),不计空气阻力,重力加速度g取10m/s2.求: