题目内容
12.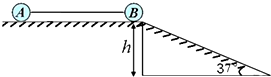 如图所示,光滑水平面与倾角为θ=37°光滑斜面平滑连接,斜面高度为h=5m,质量为mA=3kg的物体A与质量为mB=1kg的物体B通过长为2.5h轻绳连接,开始时,轻绳刚好绷直,物体B位于水平面边缘,由于受到轻微扰动,物体B由静止开始沿斜面下滑,当滑到斜面底端时,由于某种原因轻绳与AB脱离.物体A和B均可看成质点,g取10m/s2.求:(取sin37°=0.6,cos37°=0.8;AB可视为质点.)
如图所示,光滑水平面与倾角为θ=37°光滑斜面平滑连接,斜面高度为h=5m,质量为mA=3kg的物体A与质量为mB=1kg的物体B通过长为2.5h轻绳连接,开始时,轻绳刚好绷直,物体B位于水平面边缘,由于受到轻微扰动,物体B由静止开始沿斜面下滑,当滑到斜面底端时,由于某种原因轻绳与AB脱离.物体A和B均可看成质点,g取10m/s2.求:(取sin37°=0.6,cos37°=0.8;AB可视为质点.)(1)B刚好滑到斜面底端时,物体A的速度;
(2)此过程中绳对物体B所做的功;
(3)求物体A与斜面碰撞前离斜面的最远距离.
分析 (1)对AB系统由机械能守恒定律可求得小球的速度;
(2)对B球由动能定理可求得拉力所做的功;
(3)根据运动的合成与分解规律可知小球离斜面最远时沿斜面方向上的速度为零;建立直角坐标系,由运动的合成与分解可求得最远距离.
解答  解:(1)对AB系统由机械能守恒定律可知:
解:(1)对AB系统由机械能守恒定律可知:
mBgh=$\frac{1}{2}$(mA+mB)v2
代入数据解得:v=5m/s;
(2)对B由动能定理可知:
mBgh+WT=$\frac{1}{2}$mBv2-0
解得:WT=-37.5J;
(3)如图建立坐标系:
在y轴上:
vy=vsin37°
Gy=mgcos37°
沿垂直斜面方向上加速度gy=gcos37°
hy=$\frac{{v}_{y}^{2}}{2{g}_{y}}$=$\frac{9}{16}$
答:(1)B刚好滑到斜面底端时,物体A的速度为5m/s
(2)此过程中绳对物体B所做的功-37.5J;
(3)求物体A与斜面碰撞前离斜面的最远距离为$\frac{9}{16}$.
点评 本题考查动能定理、机械能守恒及运动的合成与分解,要注意正确分析物理过程,明确小球受力情况;根据题意选择合适的物理规律求解.

练习册系列答案
相关题目
7. 如图所示,竖直平面内的轨道Ⅰ和轨道Ⅱ都由两段细直杆连接而成,两轨道长度相等.用相同的水平恒力将穿在轨道最低点B的静止小球分别沿Ⅰ和Ⅱ拉至最高点A,所需时间分别为t1、t2,动能增量分别为△Ek1、△Ek2.假定球在经过轨道转折点前后速度的大小不变,若球与Ⅰ、Ⅱ轨道间接触面光滑,则( )
如图所示,竖直平面内的轨道Ⅰ和轨道Ⅱ都由两段细直杆连接而成,两轨道长度相等.用相同的水平恒力将穿在轨道最低点B的静止小球分别沿Ⅰ和Ⅱ拉至最高点A,所需时间分别为t1、t2,动能增量分别为△Ek1、△Ek2.假定球在经过轨道转折点前后速度的大小不变,若球与Ⅰ、Ⅱ轨道间接触面光滑,则( )
 如图所示,竖直平面内的轨道Ⅰ和轨道Ⅱ都由两段细直杆连接而成,两轨道长度相等.用相同的水平恒力将穿在轨道最低点B的静止小球分别沿Ⅰ和Ⅱ拉至最高点A,所需时间分别为t1、t2,动能增量分别为△Ek1、△Ek2.假定球在经过轨道转折点前后速度的大小不变,若球与Ⅰ、Ⅱ轨道间接触面光滑,则( )
如图所示,竖直平面内的轨道Ⅰ和轨道Ⅱ都由两段细直杆连接而成,两轨道长度相等.用相同的水平恒力将穿在轨道最低点B的静止小球分别沿Ⅰ和Ⅱ拉至最高点A,所需时间分别为t1、t2,动能增量分别为△Ek1、△Ek2.假定球在经过轨道转折点前后速度的大小不变,若球与Ⅰ、Ⅱ轨道间接触面光滑,则( )| A. | △Ek1>△Ek2 | B. | △Ek1=△Ek2 | C. | t1>t2 | D. | t1<t2 |
4.2006年8月24日晚,国际天文学联合会大会投票,通过了新的行星定义,冥王星被排除在行星行列之外,太阳系行星数量将由九颗减为八颗.若将八大行星绕太阳运行的轨道粗略地认为是圆,各星球半径和轨道半径如表所示
从表中所列数据可以估算出土星的公转周期最接近( )
| 行星名称 | 水星 | 金星 | 地球 | 火星 | 木星 | 土星 | 天王星 | 海王星 |
| 星球半径 (×106 m) | 2.44 | 6.05 | 6.37 | 3.39 | 69.8 | 58.2 | 23.7 | 22.4 |
| 轨道半径 (×1011 m) | 0.579 | 1.08 | 1.50 | 2.28 | 7.78 | 14.3 | 28.7 | 45.0 |
| A. | 10年 | B. | 30年 | C. | 50年 | D. | 100年 |
11. 如图所示,在倾角为α的光滑斜面上,垂直纸面放置一根直导体棒,在导体棒中通有垂直纸面向里的电流,图中a点在导体棒正下方,b点与导体棒的连线与斜面垂直,c点在a点左侧,d点在b点右侧.现欲使导体棒静止在斜面上,下列措施可行的是( )
如图所示,在倾角为α的光滑斜面上,垂直纸面放置一根直导体棒,在导体棒中通有垂直纸面向里的电流,图中a点在导体棒正下方,b点与导体棒的连线与斜面垂直,c点在a点左侧,d点在b点右侧.现欲使导体棒静止在斜面上,下列措施可行的是( )
 如图所示,在倾角为α的光滑斜面上,垂直纸面放置一根直导体棒,在导体棒中通有垂直纸面向里的电流,图中a点在导体棒正下方,b点与导体棒的连线与斜面垂直,c点在a点左侧,d点在b点右侧.现欲使导体棒静止在斜面上,下列措施可行的是( )
如图所示,在倾角为α的光滑斜面上,垂直纸面放置一根直导体棒,在导体棒中通有垂直纸面向里的电流,图中a点在导体棒正下方,b点与导体棒的连线与斜面垂直,c点在a点左侧,d点在b点右侧.现欲使导体棒静止在斜面上,下列措施可行的是( )| A. | 在a处放置一电流方向垂直纸面向外的直导体棒 | |
| B. | 在b处放置一电流方向垂直纸面向里的直导体棒 | |
| C. | 在c处放置一电流方向垂直纸面向里的直导体棒 | |
| D. | 在d处放置一电流方向垂直纸面向里的直导体棒 |


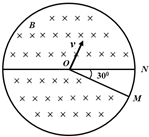 如图所示,在圆形区域中圆心角为30°的扇面MON之外分布着垂直于纸面向里的匀强磁场,磁感应强度大小为B,一质量为m、带电量为-q的粒子,自圆心O点垂直于OM以速度v射入磁场,粒子恰能两次经过边界OM,不计粒子重力.
如图所示,在圆形区域中圆心角为30°的扇面MON之外分布着垂直于纸面向里的匀强磁场,磁感应强度大小为B,一质量为m、带电量为-q的粒子,自圆心O点垂直于OM以速度v射入磁场,粒子恰能两次经过边界OM,不计粒子重力. 如图所示,匀强磁场的磁感应强度大小B=1T,方向垂直纸面向里,有一条与磁场方向垂直的长度L=1m的通电直导线,电流大小I=2.0A,方向如图所示.则导线受到的安培力大小F=2N,在图中标出F的方向.
如图所示,匀强磁场的磁感应强度大小B=1T,方向垂直纸面向里,有一条与磁场方向垂直的长度L=1m的通电直导线,电流大小I=2.0A,方向如图所示.则导线受到的安培力大小F=2N,在图中标出F的方向.
