题目内容
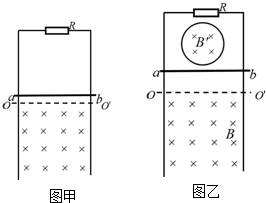
1. 在水平面上平行放置着两根长度均为L=5m的金属导轨MN和PQ,导轨间距为d=2m,导轨和电路的连接如图所示.在导轨的MP端放置着一根金属棒,与导舅垂直且接触良好.空间中存在竖直向上方向的匀强磁场,磁感应强度为B=1T.将开关S1闭合,S2断开,电压表和电流表的示数分别为U1=1V和I1=0.5A,金属棒仍处于静止状态;再将开关S2闭合,电流表的示数为I2=3.5A,金属棒在导轨上由静止开始运动,运动过程中金属棒始终与导轨垂直.设金属棒的质量为m=2kg,金属棒与导轨之间的动摩擦因数为μ=0.1.忽略导轨的电阻以及金属棒运动过程中产生的感应电动势,重力加速度为g=10m/s2.求:
在水平面上平行放置着两根长度均为L=5m的金属导轨MN和PQ,导轨间距为d=2m,导轨和电路的连接如图所示.在导轨的MP端放置着一根金属棒,与导舅垂直且接触良好.空间中存在竖直向上方向的匀强磁场,磁感应强度为B=1T.将开关S1闭合,S2断开,电压表和电流表的示数分别为U1=1V和I1=0.5A,金属棒仍处于静止状态;再将开关S2闭合,电流表的示数为I2=3.5A,金属棒在导轨上由静止开始运动,运动过程中金属棒始终与导轨垂直.设金属棒的质量为m=2kg,金属棒与导轨之间的动摩擦因数为μ=0.1.忽略导轨的电阻以及金属棒运动过程中产生的感应电动势,重力加速度为g=10m/s2.求:(1)金属棒到达NQ端时的速度大小.
(2)金属棒在导轨上运动的过程中,电流在金属棒中产生的热量.
分析 (1)根据牛顿第二定律与运动学公式,即可求解金属棒到达NQ端时的速度大小;
(2)根据焦耳定律与运动学公式,即可求解.
解答 解:(1)当通过金属棒的电流为I2时,金属棒在导轨上做匀加速运动,
设加速度为a,根据牛顿第二定律,BdI2-μmg=ma
a=2.5m/s2
设金属棒到达NQ端时的速率为v,根据运动学公式,v2=2aL;
由以上两式解得:v=$\sqrt{\frac{2(Bd{I}_{2}-μmg)L}{m}}$
代入数据解得:v=5m/s
(2)当金属棒静止不动时,金属棒的电阻r=$\frac{{U}_{1}}{{I}_{1}}$=$\frac{1}{0.5}$=2Ω,设金属棒在导轨上运动的时间为t,
电流在金属棒中产生的热量为Q,根据焦耳定律,Q=I22rt;
根据运动学公式,L=$\frac{vt}{2}$,
解得时间t=$\frac{2L}{v}$将(1)的结果代入,解得
Q=I22r$\sqrt{\frac{2Lm}{Bd{I}_{2}-μmg}}$
代入数据解得:Q=49J.
答:(1)金属棒到达NQ端时的速度大小为5m/s;
(2)金属棒在导轨上运动的过程中,电流在金属棒中产生的热量为49J.
点评 本题考查牛顿第二定律与运动学公式及焦耳定律的应用,掌握安培力的大小与方向的正确运用,要注意在求解产生的热量时,可以利用焦耳定律或者直接利用功能关系进行分析求解.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
18.伟大的物理学家伽利略探究物体下落规律的研究方法对于后来的科学研究具有重大的启蒙作用,至今仍然具有重要意义.请你回顾伽利略探究物体下落规律的过程,把下面的重要探究过程按顺序排列正确的是( )
①实验验证 ②遇到问题 ③数学推理 ④提出猜想 ⑤合理外推 ⑥得出结论.
①实验验证 ②遇到问题 ③数学推理 ④提出猜想 ⑤合理外推 ⑥得出结论.
| A. | ②④①⑤③⑥ | B. | ②④①③⑥⑤ | C. | ②④③①⑤⑥ | D. | ②①④③⑥⑤ |
19.如图所示是一质点做直线运动的v-t图象,据此图象得到的结论是( )


| A. | 质点在第1秒末停止运动 | B. | 质点在前2秒内的位移为零 | ||
| C. | 质点在第1秒末改变运动方向 | D. | 质点在第2秒内做减速运动 |
16.真空中两个相同的带等量同种电荷的金属小球A和B(均可看作点电荷),分别固定在两处,两球间静电力为F.现用一个不带电与A和B相同的金属小球C先与A接触,再与B接触,然后移开C,再使A、B间距离增大为原来两倍,则A、B两球间的静电力( )
| A. | 表现为引力且是$\frac{F}{8}$ | B. | 表现为斥力且是$\frac{F}{32}$ | ||
| C. | 表现为斥力且是$\frac{3F}{32}$ | D. | 表现为斥力且是$\frac{F}{8}$ |
3.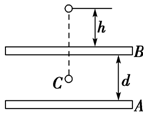 如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )
如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )
 如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )
如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )| A. | 微粒下落过程中重力做功为mg(h+$\frac{d}{2}$),电场力做功为$\frac{qU}{2}$ | |
| B. | 微粒落入电场中,电势能逐渐增大,其增加量为$\frac{qU}{2}$ | |
| C. | 若微粒从距B板高2h处自由下落,则恰好能达到A板 | |
| D. | 微粒在下落过程中动能逐渐增加,重力势能逐渐减小 |
6. 如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界的匀强磁场区域,v2=2v1,在先后两种情况下( )
如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界的匀强磁场区域,v2=2v1,在先后两种情况下( )
 如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界的匀强磁场区域,v2=2v1,在先后两种情况下( )
如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界的匀强磁场区域,v2=2v1,在先后两种情况下( )| A. | 线圈中的感应电流之比I1:I2=1:2 | |
| B. | 作用在线圈上的外力大小之比F1:F2=1:2 | |
| C. | 线圈中产生的焦耳热之比Q1:Q2=2:1 | |
| D. | 通过线圈某一截面的电荷量之比q1:q2=1:1 |
 质量为的m=1Kg、长度足够长的木板放在光滑的水平面上,右端到竖直档板的距离L=0.08m.现有一质量也为m的滑块以v0=3m/s的水平速度从板的左端滑上木板,滑块与木板间的摩擦系数为μ=0.1,滑块与档板始终未碰撞.木板与档板碰后速度大小不变,方向相反.(碰撞时间极短,忽略不计)则木板碰撞3次后木板与滑块已达到共同速度;木板与档板共碰4次,滑块在木板上发生相对的时间是3s,相对滑动距离是4.5m.
质量为的m=1Kg、长度足够长的木板放在光滑的水平面上,右端到竖直档板的距离L=0.08m.现有一质量也为m的滑块以v0=3m/s的水平速度从板的左端滑上木板,滑块与木板间的摩擦系数为μ=0.1,滑块与档板始终未碰撞.木板与档板碰后速度大小不变,方向相反.(碰撞时间极短,忽略不计)则木板碰撞3次后木板与滑块已达到共同速度;木板与档板共碰4次,滑块在木板上发生相对的时间是3s,相对滑动距离是4.5m. 如图所示,固定放置的两光滑平行金属导轨,间距d=0.2m,在桌面上的部分是水平的,处在磁感应强度B=0.1T、方向竖直向下的有界磁场中.电阻R=3Ω.桌面高H=0.8m,金属杆ab质量m=0.2kg,电阻r=1Ω,在导轨上距桌面h=0.2m的高处由静止释放,运动过程中a、b两端始终与导轨接触良好并且高度相同.落地点距桌面左边缘的水平距离s=0.4m,g=10m/s2.求:
如图所示,固定放置的两光滑平行金属导轨,间距d=0.2m,在桌面上的部分是水平的,处在磁感应强度B=0.1T、方向竖直向下的有界磁场中.电阻R=3Ω.桌面高H=0.8m,金属杆ab质量m=0.2kg,电阻r=1Ω,在导轨上距桌面h=0.2m的高处由静止释放,运动过程中a、b两端始终与导轨接触良好并且高度相同.落地点距桌面左边缘的水平距离s=0.4m,g=10m/s2.求: