题目内容
8. 如图长为L的很细的绝缘杆均匀带有正电荷,电荷在杆子内部左方$\frac{L}{4}$处的A点产生的场强为E1,在杆外部右方$\frac{L}{4}$的B点产生的场强为E2,若将杆子由中间截断,并将右段叠在左段上,则此时A处的场强为0,B处的场强为$2({E}_{2}^{\;}-{E}_{1}^{\;})$.
如图长为L的很细的绝缘杆均匀带有正电荷,电荷在杆子内部左方$\frac{L}{4}$处的A点产生的场强为E1,在杆外部右方$\frac{L}{4}$的B点产生的场强为E2,若将杆子由中间截断,并将右段叠在左段上,则此时A处的场强为0,B处的场强为$2({E}_{2}^{\;}-{E}_{1}^{\;})$.
分析 根据静电平衡状态的导体内部场强为0,得到右半部分在A点的场强,A点和B点距右半部分距离相等,右半部分在B点的场强等于右半部分在A点的场强,将杆子截断,右端叠放到左端上,根据电场的叠加和对称性原理,即可求出A、B处的场强;
解答 解:根据处于静电平衡状态的导体内部场强为0,左半部分杆子由对称性知在A点的场强为0,右半部分杆子在A点场强${E}_{1}^{\;}$;B点到右半部分距离为$\frac{L}{4}$,右半部分在B点的场强${E}_{1}^{\;}$,根据电场的叠加,杆子的左半部分在B点的场强为$({E}_{2}^{\;}-{E}_{1}^{\;})$,将杆子由中间截断,将右端叠放在左段上,根据对称性,A点的合场强为0,相当于左半部分的电荷量为原来的2倍,B处场强为$2({E}_{2}^{\;}-{E}_{1}^{\;})$
故答案为:0 $2({E}_{2}^{\;}-{E}_{1}^{\;})$
点评 因为只学过点电荷的电场或者匀强电场,而对于杆产生的电场却没有学过,因而需要将杆看成是由若干个点构成,再进行矢量合成.同时考查电场强度的叠加.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
6.下列关于匀变速直线运动的说法,正确的是( )
| A. | 它是速度均匀变化的直线运动 | |
| B. | 它是加速度均匀变化的直线运动 | |
| C. | 匀变速直线运动的v-t图象是一条平行于时间轴的直线 | |
| D. | 匀变速直线运动的加速度是一个恒量 |
3.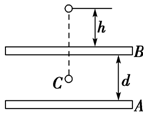 如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )
如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )
 如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )
如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )| A. | 微粒下落过程中重力做功为mg(h+$\frac{d}{2}$),电场力做功为$\frac{qU}{2}$ | |
| B. | 微粒落入电场中,电势能逐渐增大,其增加量为$\frac{qU}{2}$ | |
| C. | 若微粒从距B板高2h处自由下落,则恰好能达到A板 | |
| D. | 微粒在下落过程中动能逐渐增加,重力势能逐渐减小 |
3. 抗日战争时期,一运送物资的日军军车沿直线公路AB以速度v0匀速运动,我八路军驻地位于P处且与该公路的垂直距离PN为s,如图所示.当日军军车位于与八路军驻地相距为$\sqrt{2}$s的M处时,八路军得到情报并立即派出小分队沿直线以$\sqrt{2}$v0的速度前往拦截,若恰好成功拦截,则( )
抗日战争时期,一运送物资的日军军车沿直线公路AB以速度v0匀速运动,我八路军驻地位于P处且与该公路的垂直距离PN为s,如图所示.当日军军车位于与八路军驻地相距为$\sqrt{2}$s的M处时,八路军得到情报并立即派出小分队沿直线以$\sqrt{2}$v0的速度前往拦截,若恰好成功拦截,则( )
 抗日战争时期,一运送物资的日军军车沿直线公路AB以速度v0匀速运动,我八路军驻地位于P处且与该公路的垂直距离PN为s,如图所示.当日军军车位于与八路军驻地相距为$\sqrt{2}$s的M处时,八路军得到情报并立即派出小分队沿直线以$\sqrt{2}$v0的速度前往拦截,若恰好成功拦截,则( )
抗日战争时期,一运送物资的日军军车沿直线公路AB以速度v0匀速运动,我八路军驻地位于P处且与该公路的垂直距离PN为s,如图所示.当日军军车位于与八路军驻地相距为$\sqrt{2}$s的M处时,八路军得到情报并立即派出小分队沿直线以$\sqrt{2}$v0的速度前往拦截,若恰好成功拦截,则( )| A. | 八路军小分队的运动方向与PN夹角为30°,并指向A侧 | |
| B. | 八路军小分队的运动方向与PN夹角为45°,并指向A侧 | |
| C. | 八路军小分队经时间t=$\frac{s}{{v}_{0}}$时,恰好与日军军车相遇 | |
| D. | 八路军小分队经时间t=$\frac{(\sqrt{3}-1)s}{{v}_{0}}$时,恰好与日军军车相遇 |
20. 如图所示,边长为L、电阻不计的n匝正方形金属线框位于竖直平面内,连接的小灯泡的额定功率、额定电压分别为P、U,线框及小灯泡的总质量为m,在线框的下方有一匀强磁场区域,区域宽度为l,磁感应强度方向与线框平面垂直,其上、下边界与线框底边均水平.线框从图示位置开始静止下落,穿越磁场的过程中,小灯泡始终正常发光.则( )
如图所示,边长为L、电阻不计的n匝正方形金属线框位于竖直平面内,连接的小灯泡的额定功率、额定电压分别为P、U,线框及小灯泡的总质量为m,在线框的下方有一匀强磁场区域,区域宽度为l,磁感应强度方向与线框平面垂直,其上、下边界与线框底边均水平.线框从图示位置开始静止下落,穿越磁场的过程中,小灯泡始终正常发光.则( )
 如图所示,边长为L、电阻不计的n匝正方形金属线框位于竖直平面内,连接的小灯泡的额定功率、额定电压分别为P、U,线框及小灯泡的总质量为m,在线框的下方有一匀强磁场区域,区域宽度为l,磁感应强度方向与线框平面垂直,其上、下边界与线框底边均水平.线框从图示位置开始静止下落,穿越磁场的过程中,小灯泡始终正常发光.则( )
如图所示,边长为L、电阻不计的n匝正方形金属线框位于竖直平面内,连接的小灯泡的额定功率、额定电压分别为P、U,线框及小灯泡的总质量为m,在线框的下方有一匀强磁场区域,区域宽度为l,磁感应强度方向与线框平面垂直,其上、下边界与线框底边均水平.线框从图示位置开始静止下落,穿越磁场的过程中,小灯泡始终正常发光.则( )| A. | 有界磁场宽度l<L | |
| B. | 线框匀速穿越磁场,速度恒为$\frac{P}{mg}$ | |
| C. | 磁场的磁感应强度应为$\frac{mgU}{PL}$ | |
| D. | 线框穿越磁场的过程中,线框克服安培力做的功为2mgL |
17.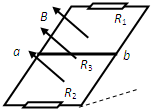 倾斜光滑、足够长的平行导轨处在匀强磁场中,导轨上的电阻R1=3Ω,下边接一最大电阻为6Ω的滑动变阻器R2,金属棒ab的质量为m、电阻R3=4Ω,其余电阻不计,斜面的斜角为α.则金属棒ab沿着导轨加速下滑的过程中( )
倾斜光滑、足够长的平行导轨处在匀强磁场中,导轨上的电阻R1=3Ω,下边接一最大电阻为6Ω的滑动变阻器R2,金属棒ab的质量为m、电阻R3=4Ω,其余电阻不计,斜面的斜角为α.则金属棒ab沿着导轨加速下滑的过程中( )
 倾斜光滑、足够长的平行导轨处在匀强磁场中,导轨上的电阻R1=3Ω,下边接一最大电阻为6Ω的滑动变阻器R2,金属棒ab的质量为m、电阻R3=4Ω,其余电阻不计,斜面的斜角为α.则金属棒ab沿着导轨加速下滑的过程中( )
倾斜光滑、足够长的平行导轨处在匀强磁场中,导轨上的电阻R1=3Ω,下边接一最大电阻为6Ω的滑动变阻器R2,金属棒ab的质量为m、电阻R3=4Ω,其余电阻不计,斜面的斜角为α.则金属棒ab沿着导轨加速下滑的过程中( )| A. | 金属棒克服安培力做的功等于其机械能的减少量 | |
| B. | 重力和安培力对金属棒做功之和等于金属棒增加的动能、电路产生的热量之和 | |
| C. | 滑动变阻器接入电路的电阻越小,金属棒匀速运动时受到的安培力越大 | |
| D. | 改变滑动变阻器接入电路的电阻,当金属棒匀速运动后R1的电功率最大时,R1、R2、R3的功率之比为P1:P2:P3=2:1:6 |
 某物理兴趣小组的同学在研究弹簧的弹力与弹簧的伸长量(或压缩量)的关系时,测得弹簧弹力的大小F和弹簧长度L的关系如图所示,则由图线可知:
某物理兴趣小组的同学在研究弹簧的弹力与弹簧的伸长量(或压缩量)的关系时,测得弹簧弹力的大小F和弹簧长度L的关系如图所示,则由图线可知: 质量为的m=1Kg、长度足够长的木板放在光滑的水平面上,右端到竖直档板的距离L=0.08m.现有一质量也为m的滑块以v0=3m/s的水平速度从板的左端滑上木板,滑块与木板间的摩擦系数为μ=0.1,滑块与档板始终未碰撞.木板与档板碰后速度大小不变,方向相反.(碰撞时间极短,忽略不计)则木板碰撞3次后木板与滑块已达到共同速度;木板与档板共碰4次,滑块在木板上发生相对的时间是3s,相对滑动距离是4.5m.
质量为的m=1Kg、长度足够长的木板放在光滑的水平面上,右端到竖直档板的距离L=0.08m.现有一质量也为m的滑块以v0=3m/s的水平速度从板的左端滑上木板,滑块与木板间的摩擦系数为μ=0.1,滑块与档板始终未碰撞.木板与档板碰后速度大小不变,方向相反.(碰撞时间极短,忽略不计)则木板碰撞3次后木板与滑块已达到共同速度;木板与档板共碰4次,滑块在木板上发生相对的时间是3s,相对滑动距离是4.5m. 粗细均匀的两端开口的U形细玻璃管开口向下竖直放置时,在左、右管中各有长度是L的水银柱封闭住总长是8L的气柱A,如图,左、右管之间的距离忽略不计,左、右管长度都是6L,两水银柱的下表面到管口距离相等.大气压保持为p=4ρgL,ρ是水银的密度,g是重力加速度.把一侧的管口封住(不计厚度),再缓慢转动U形管,使其开口向上竖直放置,两侧水银柱的长度不变.
粗细均匀的两端开口的U形细玻璃管开口向下竖直放置时,在左、右管中各有长度是L的水银柱封闭住总长是8L的气柱A,如图,左、右管之间的距离忽略不计,左、右管长度都是6L,两水银柱的下表面到管口距离相等.大气压保持为p=4ρgL,ρ是水银的密度,g是重力加速度.把一侧的管口封住(不计厚度),再缓慢转动U形管,使其开口向上竖直放置,两侧水银柱的长度不变.