题目内容
3. 如图所示放在水平地面的斜面体,斜面上用轻绳系一个质量为6kg的小球.系绳与斜面平行,斜面的倾斜角为45°,不计斜面的摩擦(g=10m/s2)求:
如图所示放在水平地面的斜面体,斜面上用轻绳系一个质量为6kg的小球.系绳与斜面平行,斜面的倾斜角为45°,不计斜面的摩擦(g=10m/s2)求:(1)当斜面以多大的加速度向右匀加速运动时小球恰好飞离斜面?
(2)当斜面以a=15m/s2运动时,绳对球的拉力是多少?
分析 首先判断小球是否飞离了斜面,根据小球刚刚飞离斜面的临界条件,即绳子的倾角不变,斜面的支持力刚好为零,解出此时的加速度与题目给出的加速度大小进行比较,若给出加速度大于小球的临界加速度说明小球已经飞离了斜面,否则小球还在斜面上.
解答 解:设小球刚刚脱离斜面时,斜面向右的加速度为a0,
此时斜面对小球的支持力恰好为零,小球只受重力和细绳的拉力,
且细绳仍然与斜面平行,小球受力如图所示,
由牛顿第二定律得:mgcotθ=ma0,
解得临界加速度:a0=gcotθ=7.5 m/s2.
加速度a=15 m/s2>a0,
则小球已离开斜面,斜面的支持力F1=0,此时小球受力如图所示:
水平方向,由牛顿第二定律得:Tcosα=ma,
竖直方向,由平衡条件得:Tsinα=mg,
解得:T=$5\sqrt{13}$ N,方向沿着细绳向上.
答:(1)当斜面以7.5 m/s2的加速度向右匀加速运动时小球恰好飞离斜面;
(2)当斜面以a=15m/s2运动时,绳对球的拉力是$5\sqrt{13}$N.
点评 此题最难解决的问题是小球是否飞离了斜面,我们可以用假设法判断出临界加速度来进行比较.

练习册系列答案
相关题目
11. 如图所示的电路中,闭合开关,灯L1、L2正常发光.由于电路出现故障,突然发现L1变亮,L2变暗,电流表的读数变小,根据分析,发生的故障可能是( )
如图所示的电路中,闭合开关,灯L1、L2正常发光.由于电路出现故障,突然发现L1变亮,L2变暗,电流表的读数变小,根据分析,发生的故障可能是( )
 如图所示的电路中,闭合开关,灯L1、L2正常发光.由于电路出现故障,突然发现L1变亮,L2变暗,电流表的读数变小,根据分析,发生的故障可能是( )
如图所示的电路中,闭合开关,灯L1、L2正常发光.由于电路出现故障,突然发现L1变亮,L2变暗,电流表的读数变小,根据分析,发生的故障可能是( )| A. | R2断路 | B. | R1断路 | C. | R3短路 | D. | R4短路 |
12. 安徽“淮南之眼”摩天轮是亚洲最高的山体摩天轮,如图所示,一质量为m的乘客坐在摩天轮中以速率v,在竖直平面内做半径为R的匀速圆周运动,假设t=0时刻乘客在轨迹最低点且重力势能为零,那么,乘客运动过程中( )
安徽“淮南之眼”摩天轮是亚洲最高的山体摩天轮,如图所示,一质量为m的乘客坐在摩天轮中以速率v,在竖直平面内做半径为R的匀速圆周运动,假设t=0时刻乘客在轨迹最低点且重力势能为零,那么,乘客运动过程中( )
 安徽“淮南之眼”摩天轮是亚洲最高的山体摩天轮,如图所示,一质量为m的乘客坐在摩天轮中以速率v,在竖直平面内做半径为R的匀速圆周运动,假设t=0时刻乘客在轨迹最低点且重力势能为零,那么,乘客运动过程中( )
安徽“淮南之眼”摩天轮是亚洲最高的山体摩天轮,如图所示,一质量为m的乘客坐在摩天轮中以速率v,在竖直平面内做半径为R的匀速圆周运动,假设t=0时刻乘客在轨迹最低点且重力势能为零,那么,乘客运动过程中( )| A. | 重力势能随时间的变化关系为Ep=mgRcos$\frac{v}{R}$t | |
| B. | 在最高点受到座位的支持力为m$\frac{{v}^{2}}{R}$-mg | |
| C. | 机械能守恒且为E=$\frac{1}{2}$mv2 | |
| D. | 机械能随时间的变化关系为E=$\frac{1}{2}$mv2+mgR(1-cos$\frac{v}{R}$t) |
3.用一个大小恒定、方向始终与运动方向相同的水平力F推小车沿半径为R的圆周运动一周,则人做的功为( )
| A. | 0 | B. | 2πR F | C. | 2R F | D. | 无法确定 |
 如图所示,在x轴上方有一匀强电场,场强大小为E,方向竖直向下,在x轴下方有一匀强磁场,磁感强度为B,方向垂直纸面向里.在x轴上有一点P,离原点距离为a,现有一带电量为正q,质量为m的粒子,从0<x<a区间某点由静止开始释放后,能经过P点,试讨论释放点坐标x、y应满足什么关系?(E、B均在x>0区域,粒子重力不计)
如图所示,在x轴上方有一匀强电场,场强大小为E,方向竖直向下,在x轴下方有一匀强磁场,磁感强度为B,方向垂直纸面向里.在x轴上有一点P,离原点距离为a,现有一带电量为正q,质量为m的粒子,从0<x<a区间某点由静止开始释放后,能经过P点,试讨论释放点坐标x、y应满足什么关系?(E、B均在x>0区域,粒子重力不计)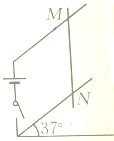 如图所示,电源、开关与光滑的金属导轨相连,导轨与水平方向成37°角放置,当导线MN放于导轨上时接通电源,通过MN的电流可达5A,把整个装置放在竖直方向的匀强磁场中,则MN刚好静止,试确定磁场的大小与方向.(MN的质量为10g,长为20m)
如图所示,电源、开关与光滑的金属导轨相连,导轨与水平方向成37°角放置,当导线MN放于导轨上时接通电源,通过MN的电流可达5A,把整个装置放在竖直方向的匀强磁场中,则MN刚好静止,试确定磁场的大小与方向.(MN的质量为10g,长为20m)