题目内容
12.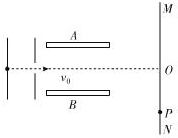 初速度为零的质子经U1=5000V的加速电压加速后,沿着平行金属板A、B的中心线进入平行板间的匀强电场,如图所示,若板间距离d=1.0cm,板长l=5.0cm.距离平行金属板s=5.0cm处有荧光屏MN,当AB间不加电压时,质子打到荧光屏的O点.
初速度为零的质子经U1=5000V的加速电压加速后,沿着平行金属板A、B的中心线进入平行板间的匀强电场,如图所示,若板间距离d=1.0cm,板长l=5.0cm.距离平行金属板s=5.0cm处有荧光屏MN,当AB间不加电压时,质子打到荧光屏的O点.(1)要使质子能从平行板间飞出,两个极板AB上最多能加多大电压?
(2)当AB间电压UAB=200V时,质子打到荧光屏上的P点,求OP大小是多少?
(3)如果换成初速度为零的α粒子,打到荧光屏上的点离P点多远?
分析 (1)根据动能定理求解粒子进入偏转电场的速度,根据牛顿第二定律求解在偏转电场中的加速度,再根据位移时间关系求解最大电压;
(2)根据类平抛运动的特点可知,速度方向反向延长线过水平位移的中点,根据三角形相似求解OP距离;
(3)推导出偏转位移的计算公式,确定偏转位移的决定因素,然后作出判断.
解答 解:(1)设质子经过加速电压加速后,获得的速度为v0,
根据动能定理可得:qU1=$\frac{1}{2}$mv02,
当质子在垂直于板面方向偏移的位移为$\frac{d}{2}$时,两板间的电压最大,设最大电压为Um,
根据牛顿第二定律可得加速度:$a=\frac{q{U}_{m}}{md}$,
在两板间运动的时间为t=$\frac{l}{{v}_{0}}$,
所以有:$\frac{d}{2}=\frac{1}{2}a{t}^{2}=\frac{1}{2}•\frac{q{U}_{m}}{md}•\frac{{l}^{2}}{{v}_{0}^{2}}=\frac{{U}_{m}{l}^{2}}{4{U}_{1}d}$,
所以${U}_{m}=\frac{2{U}_{1}{d}^{2}}{{l}^{2}}=\frac{2×5000×0.0{1}^{2}}{0.0{5}^{2}}V=400V$;
(2)当AB间电压UAB=200V时,设质子的偏转位移为y,根据类平抛运动可得:
$y=\frac{1}{2}a{t}^{2}=\frac{1}{2}•\frac{q{U}_{AB}}{md}•\frac{{l}^{2}}{{v}_{0}^{2}}=\frac{{U}_{AB}{l}^{2}}{4{U}_{1}d}$=$\frac{200×0.0{5}^{2}}{4×5000×0.01}m=2.5×1{0}^{-3}m=0.25cm$,
类平抛运动速度方向反向延长线过水平位移的中点,如图所示,
根据图中几何关系可得:$\frac{y}{OP}=\frac{\frac{l}{2}}{\frac{l}{2}+s}$,
解得:OP=0.75cm;
(3)根据$y=\frac{1}{2}a{t}^{2}=\frac{1}{2}•\frac{q{U}_{AB}}{md}•\frac{{l}^{2}}{{v}_{0}^{2}}=\frac{{U}_{AB}{l}^{2}}{4{U}_{1}d}$可得,出射时位移侧移量与粒子的比荷无关,如果换成初速度为零的α粒子,打到荧光屏上的点仍为P点.
答:(1)要使质子能从平行板间飞出,两个极板AB上最多能加多大电压为400V;
(2)当AB间电压UAB=200V时,质子打到荧光屏上的P点,求OP大小是0.75cm;
(3)如果换成初速度为零的α粒子,打到荧光屏上的点仍为P点.
点评 有关带电粒子在匀强电场中的运动,可以从两条线索展开:其一,力和运动的关系.根据带电粒子受力情况,用牛顿第二定律求出加速度,结合运动学公式确定带电粒子的速度和位移等;其二,功和能的关系.根据电场力对带电粒子做功,引起带电粒子的能量发生变化,利用动能定理进行解答.

 如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电的小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,以下说法正确的是( )
如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电的小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,以下说法正确的是( )| A. | 小球电势能的减少量等于小球重力势能的增加量 | |
| B. | 小球机械能的改变量等于电场力做的功 | |
| C. | 小球动能、电势能减少量之和等于弹性势能与小球重力势能增加量之和 | |
| D. | 弹性势能的增加量等于小球动能的减少量 |
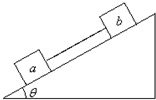 如图所示,用轻绳连接同种材料制成的a和b两个物体.a物体的质量为m1,b物体的质量为m2,m1>m2,当它们沿着有摩擦的斜面向下滑动时,连接两物体的细线的受力情况是( )
如图所示,用轻绳连接同种材料制成的a和b两个物体.a物体的质量为m1,b物体的质量为m2,m1>m2,当它们沿着有摩擦的斜面向下滑动时,连接两物体的细线的受力情况是( )| A. | 当a和b两物体匀速下滑时,细线中的拉力等于零;当a和b两物体不是匀速下滑时,细线中的拉力不等于零 | |
| B. | 当a与b两物体一起加速下滑时,b物体通过细线拉a物体向下加速运动 | |
| C. | 不论a与b是匀速运动,还是加速运动,细线中的拉力均等于零 | |
| D. | 两物体与斜面的摩擦力相等时,细线中的拉力才可能等于零 |
 如图所示是将滑动变阻器用作分压器的电路,A、B为分压器的输出端,电源电压U恒定,若把变阻器的滑片放在变阻器的中间,下列判断正确的是( )
如图所示是将滑动变阻器用作分压器的电路,A、B为分压器的输出端,电源电压U恒定,若把变阻器的滑片放在变阻器的中间,下列判断正确的是( )| A. | AB间不接负载时输出电压UAB=$\frac{U}{2}$ | |
| B. | 当AB间接上负载R时,输出电压UAB<$\frac{U}{2}$ | |
| C. | 负载电阻R越大,UAB越接近$\frac{U}{2}$ | |
| D. | 接上负载后要使UAB=$\frac{U}{2}$,则滑片P应向下移动 |
 如图所示,质量为1kg的物块在倾角为53°的固定斜面上向下滑动,若给物块施加平行于斜面向上的拉力F,则物块刚好能匀速下滑,F=5N.求:物块与斜面之间的动摩擦因数.(sin53°=0.8,cos53°=0.6,g=10N/kg)
如图所示,质量为1kg的物块在倾角为53°的固定斜面上向下滑动,若给物块施加平行于斜面向上的拉力F,则物块刚好能匀速下滑,F=5N.求:物块与斜面之间的动摩擦因数.(sin53°=0.8,cos53°=0.6,g=10N/kg) 如图所示,水平面上固定着一个半径R=0.4m的光滑圆环形轨道.在轨道内放入质量分别是M=0.2kg和m=0.1kg的小球A和B(均可看作质点),两小球间夹一轻质短弹簧(弹簧的长度相对环形轨道的半径和周长而言可忽略不计).开始时,两小球将轻质弹簧压缩,已知压缩弹簧在弹开前储存的弹性势能E=1.2J,弹簧释放后,两小球沿轨道反方向运动.
如图所示,水平面上固定着一个半径R=0.4m的光滑圆环形轨道.在轨道内放入质量分别是M=0.2kg和m=0.1kg的小球A和B(均可看作质点),两小球间夹一轻质短弹簧(弹簧的长度相对环形轨道的半径和周长而言可忽略不计).开始时,两小球将轻质弹簧压缩,已知压缩弹簧在弹开前储存的弹性势能E=1.2J,弹簧释放后,两小球沿轨道反方向运动.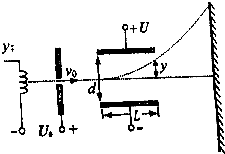 示波器是一种用途十分广泛的电子测量仪器,它的核心部件是示波管,其工作原理如图所示,初速为0的电子经过加速电压为U0的电场加速后,进入电压为U的偏转电场,然后射到荧光屏上.已知两偏转电极板间的距离为d,极板长为L,电子的质量为m,电荷量为e.不考虑电子所受重力,求:
示波器是一种用途十分广泛的电子测量仪器,它的核心部件是示波管,其工作原理如图所示,初速为0的电子经过加速电压为U0的电场加速后,进入电压为U的偏转电场,然后射到荧光屏上.已知两偏转电极板间的距离为d,极板长为L,电子的质量为m,电荷量为e.不考虑电子所受重力,求: 如图所示,区域Ⅰ、Ⅱ内存在着垂直纸面向外的匀强磁场,磁感应强度分别为B1=B,B2=0.5B.区域宽度分别为d、2d.一带正电的粒子(重力不计)从左边界上的A点垂直边界射入区域Ⅰ中,粒子的质量为m,带电量为q.
如图所示,区域Ⅰ、Ⅱ内存在着垂直纸面向外的匀强磁场,磁感应强度分别为B1=B,B2=0.5B.区域宽度分别为d、2d.一带正电的粒子(重力不计)从左边界上的A点垂直边界射入区域Ⅰ中,粒子的质量为m,带电量为q.