题目内容
17. 如图所示,区域Ⅰ、Ⅱ内存在着垂直纸面向外的匀强磁场,磁感应强度分别为B1=B,B2=0.5B.区域宽度分别为d、2d.一带正电的粒子(重力不计)从左边界上的A点垂直边界射入区域Ⅰ中,粒子的质量为m,带电量为q.
如图所示,区域Ⅰ、Ⅱ内存在着垂直纸面向外的匀强磁场,磁感应强度分别为B1=B,B2=0.5B.区域宽度分别为d、2d.一带正电的粒子(重力不计)从左边界上的A点垂直边界射入区域Ⅰ中,粒子的质量为m,带电量为q.(1)若粒子不能进入区域Ⅱ,求粒子的速度满足的条件及此种情况下粒子在区域Ⅰ中运动的时间.
(2)若粒子刚好能射出区域Ⅱ,求粒子的速度大小.
分析 (1)找到粒子不能进入区域II的临界几何条件,洛伦兹力提供向心力与几何关系结合即可;
(2)画出运动过程图,找到粒子恰好能射出区域II的临界几何条件,再与洛伦兹力提供向心力结合即可.
解答 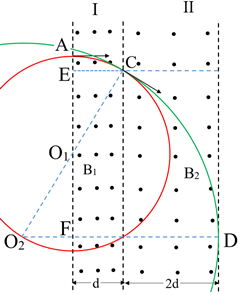
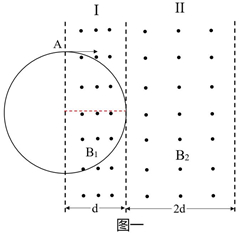 解:(1)粒子不能进入II的临界条件为粒子轨迹恰好与I、II两区域的边界相切,如图一所示
解:(1)粒子不能进入II的临界条件为粒子轨迹恰好与I、II两区域的边界相切,如图一所示
根据洛伦兹力提供向心力有:qvB1=m$\frac{{v}^{2}}{R}$ ①
粒子不能进入II区域,几何关系应满足:R≤d ②
联立①②结合已知条件得:v≤$\frac{qBd}{m}$
粒子运动的周期:T=$\frac{2πR}{v}$③
联立①③得:T=$\frac{2πm}{qB}$ ④
粒子运动的时间:t=$\frac{θ}{2π}$T ⑤
根据对称关系可知粒子垂直入射区域I,垂直穿出区域I,所以θ=π ⑥
由④⑤⑥式联立得t=$\frac{πm}{qB}$
(2)画出粒子运动过程图,如图二所示,设粒子在区域I、II中轨迹圆的半径分别为R1、R2,圆心分别为O1、O2,粒子在两个区域的轨迹恰好在C点相切,又因为粒子恰好射出区域II,所以粒子在区域II中运动的轨迹与区域II的右边界相切于D点,此时粒子恰好在D点射出区域II.
根据洛伦兹力提供向心力,在区域I中有:qvB1=m$\frac{{v}^{2}}{{R}_{1}}$ ⑦
根据洛伦兹力提供向心力,在区域II中有:qvB2=m$\frac{{v}^{2}}{{R}_{2}}$ ⑧
⑦⑧式子结合已知条件B1=B,B2=0.5B,可得:R2=2R1
根据几何关系有:△O1EC与△O1FO2全等
可得:O2F=EC=d
所以:R2=O2D=O2F+FD=4d ⑨
⑧⑨式联立得:v=$\frac{2qBd}{m}$
答:(1)若粒子不能进入区域Ⅱ,粒子的速度v应满足v≤$\frac{qBd}{m}$,粒子在区域Ⅰ中运动的时间为$\frac{πm}{qB}$.
(2)若粒子刚好能射出区域Ⅱ,求粒子的速度大小为$\frac{2qBd}{m}$.
点评 本题考查带电粒子在有界磁场中的运动,解决这类问题的思路是固定的,同学们要牢记:即洛伦兹力提供向心力与几何关系结合;解决第二问的关键在于规范作图,分析好两轨迹在C点的速度衔接关系,两轨迹圆恰好在C点内切.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案| A. | 第1 s内速度的变化量小于第2 s内速度的变化量 | |
| B. | 第1 s内速度的变化量大于第2 s内速度变化量 | |
| C. | 第1 s内位移一定小于第2 s内的位移 | |
| D. | 相邻两段相等时间内位移之差等于一个恒量 |
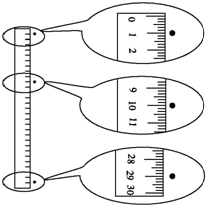 科技馆里有一个展品,该展品放在暗处,顶部有一个不断均匀向下喷射水滴的装置,在频闪光源的照射下,可以看到水滴好像静止在空中固定的位置不动,如图所示.某同学为计算该装置喷射水滴的时间间隔,用最小刻度为毫米的刻度尺测量了空中几滴水间的距离,由此可计算出该装置喷射水滴的时间间隔为(g取10m/s2)( )
科技馆里有一个展品,该展品放在暗处,顶部有一个不断均匀向下喷射水滴的装置,在频闪光源的照射下,可以看到水滴好像静止在空中固定的位置不动,如图所示.某同学为计算该装置喷射水滴的时间间隔,用最小刻度为毫米的刻度尺测量了空中几滴水间的距离,由此可计算出该装置喷射水滴的时间间隔为(g取10m/s2)( )| A. | 0.01 s | B. | 0.02 s | C. | 0.1 s | D. | 0.2 s |
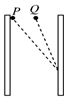 如图所示,竖直正对放置的两个平行金属板间有匀强电场,在两板之间等高处有两个质量相同的带电小球,P小球从紧靠左极板处静止释放,Q小球从两板正中央静止释放,两小球最后都打在右极板上的同一位置.则两小球从释放到打在右极板上的过程中( )
如图所示,竖直正对放置的两个平行金属板间有匀强电场,在两板之间等高处有两个质量相同的带电小球,P小球从紧靠左极板处静止释放,Q小球从两板正中央静止释放,两小球最后都打在右极板上的同一位置.则两小球从释放到打在右极板上的过程中( )| A. | 它们的运行时间tP>tQ | |
| B. | 它们的电荷量之比qP:qQ=2:1 | |
| C. | 它们的动能增加量之比△EkP:△EkQ=4:1 | |
| D. | 它们的电势能减少量之比△EP:△EQ=4:1 |
 如图所示是商场中台阶式电梯,一人静止站在电梯水平梯板OP上,跟随电梯以速度υ斜向上(平行NP)做匀速直线运动,下列关于水平梯板对人的支持力F和静摩擦力f的说法,正确的是( )
如图所示是商场中台阶式电梯,一人静止站在电梯水平梯板OP上,跟随电梯以速度υ斜向上(平行NP)做匀速直线运动,下列关于水平梯板对人的支持力F和静摩擦力f的说法,正确的是( )| A. | F垂直NP斜向上 | B. | f平行NP斜向上 | C. | f平行OP向右 | D. | f=0 |

 如图所示,离子发生器发射出一束质量为m,带电量为q的离子(初速不计),经加速电压u1加速后以垂直于电场方向射入两平行板中央,受偏转电压u2作用后,以速度v离开电场.已知平行板的长度为L,两板间距离为d,试证明
如图所示,离子发生器发射出一束质量为m,带电量为q的离子(初速不计),经加速电压u1加速后以垂直于电场方向射入两平行板中央,受偏转电压u2作用后,以速度v离开电场.已知平行板的长度为L,两板间距离为d,试证明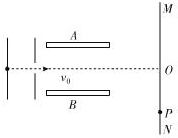 初速度为零的质子经U1=5000V的加速电压加速后,沿着平行金属板A、B的中心线进入平行板间的匀强电场,如图所示,若板间距离d=1.0cm,板长l=5.0cm.距离平行金属板s=5.0cm处有荧光屏MN,当AB间不加电压时,质子打到荧光屏的O点.
初速度为零的质子经U1=5000V的加速电压加速后,沿着平行金属板A、B的中心线进入平行板间的匀强电场,如图所示,若板间距离d=1.0cm,板长l=5.0cm.距离平行金属板s=5.0cm处有荧光屏MN,当AB间不加电压时,质子打到荧光屏的O点.