题目内容
12．一汽车通过拱形桥顶时恰对桥面没有压力，这时汽车的速度为10m/s，则拱形桥的半径为（ ）（g取10m/s2）| A． | 1m | B． | 10m | C． | 10m | D． | 20m |
分析 车对桥无压力时，重力恰好提供向心力，可由向心力公式列式求出半径．
解答 解：车在桥顶对桥面没有压力时，由重力提供向心力，则有：
mg=m$\frac{{v}^{2}}{R}$
解得：R=$\frac{{v}^{2}}{g}=\frac{100}{10}=10m$
故选：C
点评 本题关键找出向心力来源后根据向心力公式和牛顿第二定律联立列式求解．
练习册系列答案
相关题目
11．A、B两个质点，分别做匀速圆周运动，在相同的时间内它们通过的路之比sA：sB=2：3，转过的角度之比φA：φB=3：2，则下列说法正确的是（ ）
| A． | 它们的半径之比为RA：RB=2：3 | B． | 它们的半径之比为RA：RB=9：4 | ||
| C． | 它们的周期之比为TA：TB=2：3 | D． | 它们的周期之比为TA：TB=3：2 |
7．
如图所示，一带电小球从A处竖直向上进入一水平方向的匀强电场中，进入电场时小球的动能为4J，运动到最高点B时小球的动能为5J，则小球运动到与A点在同一水平面上的C点（图中未画出）时（ ）
如图所示，一带电小球从A处竖直向上进入一水平方向的匀强电场中，进入电场时小球的动能为4J，运动到最高点B时小球的动能为5J，则小球运动到与A点在同一水平面上的C点（图中未画出）时（ ）| A． | 带电小球在AB段和BC段水平位移之比为1：3 | |
| B． | 带电小球的运动轨迹为抛物线 | |
| C． | 小球运动到与A点在同一水平面上的C点时的动能为14J | |
| D． | 小球运动到与A点在同一水平面上的C点时的动能为19J |
4．
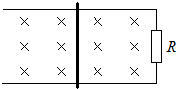如图所示间距为L的光滑平行金属导轨，水平放置在竖直方向的磁感应强度为B的匀强磁场中，一端接阻值是R的电阻．一电阻为R0、质量为m的导体棒放置在导轨上，在外力作用下从t=0的时刻开始运动，其速度随时间的变化规律v=vmsinωt，不计导轨电阻．则从t=0到t=$\frac{π}{2ω}$时间内外力F所做的功为（ ）
如图所示间距为L的光滑平行金属导轨，水平放置在竖直方向的磁感应强度为B的匀强磁场中，一端接阻值是R的电阻．一电阻为R0、质量为m的导体棒放置在导轨上，在外力作用下从t=0的时刻开始运动，其速度随时间的变化规律v=vmsinωt，不计导轨电阻．则从t=0到t=$\frac{π}{2ω}$时间内外力F所做的功为（ ）| A． | $\frac{{π{B^2}{L^2}v_m^2}}{{4ω（R+{R_0}）}}$+$\frac{1}{2}$mvm2 | B． | $\frac{{π{B^2}{L^2}v_m^2}}{{4ω（R+{R_0}）}}$ | ||
| C． | $\frac{{π{B^2}{L^2}v_m^2}}{{4ω（R+{R_0}）}}$-$\frac{1}{2}$mvm2 | D． | $\frac{{π{B^2}{L^2}v_m^2}}{{2ω（R+{R_0}）}}$ |
1．
如图所示，密闭容器内的氢气温度与外界空气的温度相同，现对该容器缓慢加热，当容器内的氢气温度高于外界空气的温度时，则（ ）
如图所示，密闭容器内的氢气温度与外界空气的温度相同，现对该容器缓慢加热，当容器内的氢气温度高于外界空气的温度时，则（ ）| A． | 氢分子的平均动能增大 | B． | 氢分子的势能增大 | ||
| C． | 容器内氢气的内能增大 | D． | 容器内氢气的内能可能不变 | ||
| E． | 容器内氢气的压强增大 |
2．
在平直的飞机跑道上进行了一次特殊比赛，飞机与摩托车同时从同一起跑线出发．图示为飞机和摩托车运动的v-t图象，则以下说法正确的是（ ）
在平直的飞机跑道上进行了一次特殊比赛，飞机与摩托车同时从同一起跑线出发．图示为飞机和摩托车运动的v-t图象，则以下说法正确的是（ ）| A． | 运动初始阶段摩托车在前，t1时刻摩托车与飞机相距最远 | |
| B． | 运动初始阶段摩托车在前，t3时刻摩托车与飞机相距最远 | |
| C． | 当飞机与摩托车再次相遇时，飞机已经达到最大速度2v0 | |
| D． | 当飞机与摩托车再次相遇时，飞机没有达到最大速度2v0 |