题目内容
6．
如图所示，物体在斜向上的恒力F作用下从静止起沿光滑水平面运动，然后在倾角为30°的光滑斜面上运动一段距离后速度变为额零．当物体在水平面和斜面上速度大小均为v时，机械能随时间的瞬时变化率分别为P1、P2，若物体在水平面和斜面上的加速度大小均为3m/s2，则（ ）| A． | P2＞0，且P1＞P2 | B． | P2＞0，且P1=P2 | C． | P2＜0，且 P1＞|P2| | D． | P2＜0，且P1=|P2| |
分析 根据功能关系知道机械能随时间的瞬时变化率等于拉力F的功率，根据功率公式和牛顿第二定律分析即可．
解答 解：由功能关系知道机械能随时间的瞬时变化率等于拉力F的功率，则
P1=Fvcosα
由牛顿第二定律得 Fcosα=ma，则P1=mav=3mv
P2=F′v，F′为F沿斜面方向的分力大小．
根据牛顿第二定律得 mgsin30°-F′=ma
将a=3m/s2，代入解得 F′=2m
则 P2=2mv，所以P1＞P2．
由于F一直做正功，所以物体的机械能一直在增大，则P2＞0，故A正确．
故选：A．
点评 解决本题的关键要明确理解功能关系，明确功率的一般公式P=Fvcosα，α是F与v的夹角．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图所示，在水平面上有质量皆为m的五个物块并排靠在一起，每个物块与地面间的动摩擦因数均为μ，相邻两物块之间均用长为s的柔软轻绳相连接（图中未画出），现用大小为F=3μmg水平恒定拉力从静止开始拉动物块1．相邻两物块之间的绳子绷紧时，绳子不会断裂也不会伸长，且绷紧时间极短．试求：
17．一端连着一个质量为m，电荷量为q的小球，以杆的另一端为圆心在匀强磁场中逆时针方向做匀速圆周运动，若小球与杆突然分离（不计重力），则速度v，半径r，周期T的不可能的情况是（ ）
| A． | v变大，r变大，T变大 | B． | v不变，r变小，T变小 | ||
| C． | v不变，r变大，T变大 | D． | v不变，r不变，T不变 |
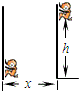如图所示，在杂技表演中，猴子沿竖直杆向上做初速度为零的匀加速运动，同时人顶着直杆水平匀速移动，若猴子经过3s时间沿杆向上滑动3.6m的高度，同时人顶杆沿水平地面移动的距离为5.4m．已知sin37°=0.6，cos37°=0.8．
金属杆MN和PQ间距为l，MP间接有电阻R，磁场如图所示，磁感应强度为B．金属棒AB长2l，由图示位置以A为轴，以角速度ω匀速转过90°求该过程中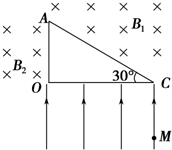
有一直角三角形OAC，OC水平且长为12 cm，其下方存在垂直OC向上的匀强电场，∠C=30°，AC上方存在垂直纸面向里的匀强磁场，磁感应强度为B1=1 T，OA左侧也存在垂直纸面向里的匀强磁场，磁感应强度B2未知，一质量为m=8×10-10kg、电荷量q=1×10-4C的带正电粒子从M点由静止释放，MC=8 cm，MC⊥OC，粒子经电场加速后进入磁场，恰好经A点到达O点，不计粒子重力，求：
18．下列关于热学现象和热学规律说法正确的是（ ）
| A． | 布朗运动就是液体分子的无规则运动 | |
| B． | 热量能从高温传到低温物体，但不可能从低温传到高温物体而不产生其他影响 | |
| C． | 物体的温度为0℃时，物体分子的平均动能为零 | |
| D． | 只要知道水的摩尔质量和水分子的质量，就可以计算出阿伏伽德罗常数 | |
| E． | 一定质量的理想气体当气体等压膨胀时，气体的内能一定增大 |
16．
2013年6月20日，我国宇航员王亚平在天宫授课时，利用质量测量仪粗略测出了聂海胜的质量．若聂海胜受恒力F的作用从静止开始运动，测出位移为x时的速度为v，则聂海胜的质量为（ ）
2013年6月20日，我国宇航员王亚平在天宫授课时，利用质量测量仪粗略测出了聂海胜的质量．若聂海胜受恒力F的作用从静止开始运动，测出位移为x时的速度为v，则聂海胜的质量为（ ）| A． | $\frac{Fx}{{v}^{2}}$ | B． | $\frac{2Fx}{{v}^{2}}$ | C． | $\frac{Fx}{{2v}^{2}}$ | D． | $\frac{\sqrt{2}Fx}{{v}^{2}}$ |
地面上方存在水平向右的匀强电场，一质量为m带电量为q的小球用绝缘丝线悬挂在电场中，当小球静止时丝线与竖直方向的夹角为θ，此时小球到地面的高度为h．求：