��Ŀ����
14��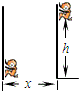 ��ͼ��ʾ�����Ӽ������У���������ֱ�����������ٶ�Ϊ����ȼ����˶���ͬʱ�˶���ֱ��ˮƽ�����ƶ��������Ӿ���3sʱ���ظ����ϻ���3.6m�ĸ߶ȣ�ͬʱ�˶�����ˮƽ�����ƶ��ľ���Ϊ5.4m����֪sin37��=0.6��cos37��=0.8��
��ͼ��ʾ�����Ӽ������У���������ֱ�����������ٶ�Ϊ����ȼ����˶���ͬʱ�˶���ֱ��ˮƽ�����ƶ��������Ӿ���3sʱ���ظ����ϻ���3.6m�ĸ߶ȣ�ͬʱ�˶�����ˮƽ�����ƶ��ľ���Ϊ5.4m����֪sin37��=0.6��cos37��=0.8����1���Ի��������ƶ��Ĺ켣��
��2����������ϻ���3.6m�߶�ʱ�ĶԵ�λ�ƴ�С��
��3����������ϻ���3.6m�߶�ʱ�ĶԵ��ٶȵĴ�С�ͷ���
���� ��1��������ֱ���˶����ȼ���ֱ���˶���ˮƽ���˶�������ֱ���˶������˶�������ƽ���˶���
��2�����ݷ�λ�ƹ�ʽ��ʽ����ˮƽ��λ�ƣ�������ƽ���ı��ζ���ϳɳ���λ�ƣ�
��3����������ƽ���˶��ķ��ٶȹ�ʽ��ʽ���ĩλ�õķ��ٶȣ�Ȼ�����ƽ���ı��ζ���ϳɳ��ٶȣ�
��� �⣺��1��������ֱ���˶����ȼ���ֱ���˶���ˮƽ���˶�������ֱ���˶����켣��ͼ��
��2���������ϻ���y=3.6m�߶ȹ��̣�ˮƽ����ǰ��x=5.4m���ʺ�λ��Ϊ��
S=$\sqrt{{x}^{2}+{y}^{2}}=\sqrt{5��{4}^{2}+3��{6}^{2}}$��6.5m
��3���������ϻ���3.6m�߶ȹ��̣�
y=$\frac{{v}_{y}}{2}t$
��ã�
${v}_{y}=\frac{2y}{t}=\frac{2��3.6}{3}$=2.4m/s
ˮƽ���ٶȣ�
${v}_{x}=\frac{x}{t}=\frac{5.4m}{3s}=1.8m/s$
�ʺ��ٶȣ�
v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}=\sqrt{1��{8}^{2}+2��{4}^{2}}=3m/s$
��ˮƽ����нǵ�����ֵ��
$tan��=\frac{{v}_{y}}{{v}_{x}}=\frac{4}{3}$
�ʦ�=53��
�𣺣�1�������ƶ��Ĺ켣��ͼ��ʾ��
��2���������ϻ���3.6m�߶�ʱ�ĶԵ�λ�ƴ�СΪ6.5m��
��3���������ϻ���3.6m�߶�ʱ�ĶԵ��ٶȵĴ�СΪ3m/s����ˮƽ����н�Ϊ53�㣮
���� ����ؼ��Dz����˶��ĺϳ���ֽ��֪ʶ�о�С���ӵ��˶����������ƽ���˶��ķ��˶���ʽ��ʽ��⣬���ѣ�

 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д�| A�� | X�����Ǵ��ڼ���̬��ԭ�Ӻ˷������ | |
| B�� | һȺ����n=3�ܼ�����̬����ԭ�ӣ��Է�ԾǨʱ�ܷ���3�ֲ�ͬƵ�ʵĹ� | |
| C�� | ������Ԫ�ط���һ�Φ�˥�䣬ԭ����������1 | |
| D�� | 235U�İ�˥��ԼΪ7���꣬������ı仯����˥�ڿ��ܱ�� |
 ��ͼ��ʾ��������б���ϵĺ���F�����´Ӿ�ֹ���ع⻬ˮƽ���˶���Ȼ�������Ϊ30��Ĺ⻬б�����˶�һ�ξ�����ٶȱ�Ϊ���㣮��������ˮƽ���б�����ٶȴ�С��Ϊvʱ����е����ʱ���˲ʱ�仯�ʷֱ�ΪP1��P2����������ˮƽ���б���ϵļ��ٶȴ�С��Ϊ3m/s2��������
��ͼ��ʾ��������б���ϵĺ���F�����´Ӿ�ֹ���ع⻬ˮƽ���˶���Ȼ�������Ϊ30��Ĺ⻬б�����˶�һ�ξ�����ٶȱ�Ϊ���㣮��������ˮƽ���б�����ٶȴ�С��Ϊvʱ����е����ʱ���˲ʱ�仯�ʷֱ�ΪP1��P2����������ˮƽ���б���ϵļ��ٶȴ�С��Ϊ3m/s2��������| A�� | P2��0����P1��P2 | B�� | P2��0����P1=P2 | C�� | P2��0���� P1��|P2| | D�� | P2��0����P1=|P2| |
| A�� | ��ѩ����·������ɳ��������Ħ�����ڳ�����ʻ | |
| B�� | Ϊ��ֹ�����Σ�����ɻ�������ϵ���̥Ҫ�õ������Ƴ� | |
| C�� | ij������������ϱ�ע���ǣ���300V 5��F�����õ�����ֻ����300 V��ѹʱ�������� | |
| D�� | ij��ͨ7��п�̸ɵ�ص�������400 mA•h����˵����40 mA����Ϊ�õ������磬���Թ���10 h |

 ��ͼ��ʾ�������ѹ��������Ȧ�ӽ���ѹU���μ���Ȧa����1�ѣ����·��һ��ͬ�����ϣ�ͬ����С����Ȧb����a�ĺ�������b��2������ʱ��ôμ���Ȧ�����·���Ӵ������ĵ�ѹΪ3.2V��������a��b��Ȧ��λ�öԵ����ٲ�μ���Ȧ�����·���Ӵ������ĵ�ѹ���Ƕ��ٷ���
��ͼ��ʾ�������ѹ��������Ȧ�ӽ���ѹU���μ���Ȧa����1�ѣ����·��һ��ͬ�����ϣ�ͬ����С����Ȧb����a�ĺ�������b��2������ʱ��ôμ���Ȧ�����·���Ӵ������ĵ�ѹΪ3.2V��������a��b��Ȧ��λ�öԵ����ٲ�μ���Ȧ�����·���Ӵ������ĵ�ѹ���Ƕ��ٷ��� һ������Ϊ5kg�����壬����v-tͼ����ͼ��ʾ����
һ������Ϊ5kg�����壬����v-tͼ����ͼ��ʾ����