题目内容
4.在利用重锤下落验证机械能守恒定律的实验中:(1)某同学在实验中得到的纸带如图所示,其中A、B、C、D是打下的相邻的四个点,它们到运动起点O的距离分别为s1、s2、s3、s4.已知当地的重力加速度为g,打点计时器所用电源频率为f,重锤质量为m.请根据以上数据计算重锤从开始下落起到打点计时器打C点的过程中,重力势能的减少量为mgs3,动能的增加量为$\frac{1}{8}m({s}_{4}-{s}_{2})^{2}{f}^{2}$.(用题目所给字母表示)

(2)甲、乙、丙三位同学分别得到A、B、C三条纸带,它们前两个打点间的距离分别是1.9mm、7.0mm、1.8mm.那么一定存在操作错误的同学是乙
(3)某同学在同一次实验中计算了多组动能的变化量△Ek,画出动能的变化量△Ek与下落的对应高度△h的关系图象,在实验误差允许的范围内,得到的△EK-△h图象应是如下图的C.

分析 (1)根据下降的高度求出重力势能的减小量,根据某段时间内的平均速度等于中间时刻的瞬时速度求出C点的速度,从而得出动能的增加量.
(2)根据自由落体运动的位移时间公式求出第1、2两点间的距离,从而确定哪一个同学操作错误.
(3)根据机械能守恒得出△Ek与△h的关系式,从而确定正确的图线.
解答 解:(1)重锤从开始下落起到打点计时器打C点的过程中,重力势能的减少量为△Ep=mgs3,C点的瞬时速度${v}_{C}=\frac{{s}_{4}-{s}_{2}}{2T}=\frac{{s}_{4}-{s}_{2}}{2}f$,则动能的增加量$△{E}_{k}=\frac{1}{2}m{{v}_{c}}^{2}$=$\frac{1}{8}m({s}_{4}-{s}_{2})^{2}{f}^{2}$.
(2)第一二点间的距离x=$\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×0.0{2}^{2}m=2mm$,可知操作一定错误的是乙同学.
(3)根据机械能守恒得,mg△h=△Ek,可知△EK-△h图象是过原点的一条倾斜直线.
故答案为:(1)mgs3,$\frac{1}{8}m({s}_{4}-{s}_{2})^{2}{f}^{2}$;(2)乙,(3)C.
点评 解决本题的关键知道实验的原理,掌握纸带的处理方法,会通过纸带求解瞬时速度,从而得出动能的增加量,会根据下降的高度求解重力势能的减小量.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图所示,游乐场中一位小朋友沿滑梯加速下滑,在此过程中他的机械能并不守恒,其原因是( )
如图所示,游乐场中一位小朋友沿滑梯加速下滑,在此过程中他的机械能并不守恒,其原因是( )
 如图所示,游乐场中一位小朋友沿滑梯加速下滑,在此过程中他的机械能并不守恒,其原因是( )
如图所示,游乐场中一位小朋友沿滑梯加速下滑,在此过程中他的机械能并不守恒,其原因是( )| A. | 因为小朋友做加速运动,所以机械能不守恒 | |
| B. | 因为小朋友受到的合力不为零,所以机械能不守恒 | |
| C. | 因为小朋友受到的合力做功不为零,所以机械能不守恒 | |
| D. | 因为除重力做功外还有摩擦阻力做功,所以机械能不守恒 |
15.下列四幅图的有关说法中正确的是( )

| A. | 甲图中,球m1以速度v碰撞静止球m2,若两球质量相等,碰后m2的速度一定为v | |
| B. | 乙图中,在光颜色保持不变的情况下,入射光越强,最大初动能越大 | |
| C. | 丙图中,射线甲由电子组成,射线乙为电磁波,射线丙由α粒子组成 | |
| D. | 丁图所示的链式反应属于重核的裂变 |
12.在水平地面上方高h=5m处以v0=5m/s的初速度平抛一小球,若空气阻力忽略不计,g=10m/s2.则( )
| A. | 小球的水平位移大小为5m | |
| B. | 小球的飞行时间为2s | |
| C. | 小球落地时速度的大小为10m/s | |
| D. | 小球落地时速度的方向与水平方向的夹角为30° |
19.在验证机械能守恒定律的实验中,某同学利用图甲中器材进行实验,正确地完成实验操作后,得到一条点迹清晰的纸带,如图乙所示.在实验数据处理中,某同学取A、B两点来验证实验.已知打点计时器每隔0.02s打一个点,g取9.8m/s2,图中测量结果记录在下面的表格中.

(1)观察纸带,可知连接重物的夹子夹在纸带的端左(选填“左”或“右”);
(2)通过计算可得vA=0.60m/s,vB=3.00m/s(结果均保留两位小数):
(3)若重物和夹子的总质量为0.5kg,那么从A到B的运动过程中,重力势能的减少量为2.21J,动能的增加量为2.16J(结果均保留二位小数);
(4)由(3)中计算出的结果你可以得到的结论是在实验误差允许的范围内,物体的机械能守恒.

| 项目 | x1/cm | A点瞬时速度/(m•s-1) | x2/cm | B点瞬时速度/(m•s-1) | A、B两点间距离/cm |
| 数据 | 2.40 | 12.00 | 45.00 |
(2)通过计算可得vA=0.60m/s,vB=3.00m/s(结果均保留两位小数):
(3)若重物和夹子的总质量为0.5kg,那么从A到B的运动过程中,重力势能的减少量为2.21J,动能的增加量为2.16J(结果均保留二位小数);
(4)由(3)中计算出的结果你可以得到的结论是在实验误差允许的范围内,物体的机械能守恒.
12. 如图,电阻不计的平行金属导轨与水平面成θ角,导轨与定值电阻R1和R2相连,匀强磁场垂直穿过整个导轨平面.有一导体棒ab,质量为m,其电阻R0与定值电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ.若使导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到的安培力大小为F,此时( )
如图,电阻不计的平行金属导轨与水平面成θ角,导轨与定值电阻R1和R2相连,匀强磁场垂直穿过整个导轨平面.有一导体棒ab,质量为m,其电阻R0与定值电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ.若使导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到的安培力大小为F,此时( )
 如图,电阻不计的平行金属导轨与水平面成θ角,导轨与定值电阻R1和R2相连,匀强磁场垂直穿过整个导轨平面.有一导体棒ab,质量为m,其电阻R0与定值电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ.若使导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到的安培力大小为F,此时( )
如图,电阻不计的平行金属导轨与水平面成θ角,导轨与定值电阻R1和R2相连,匀强磁场垂直穿过整个导轨平面.有一导体棒ab,质量为m,其电阻R0与定值电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ.若使导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到的安培力大小为F,此时( )| A. | 电阻R1的发热功率为$\frac{Fv}{3}$ | |
| B. | 电阻R0的发热功率为$\frac{Fv}{3}$ | |
| C. | 整个装置因摩擦而产生的热功率为μmgv•cosθ | |
| D. | 导体棒ab所受的安培力方向竖直向下 |
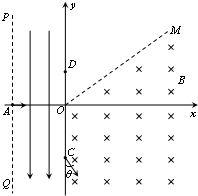 如图所示,在xOy平面内,直线PQ和y轴之间存在沿y轴负方向的匀强电场,在第四象限和第一象限的部分区域内存在垂直纸面向内的匀强磁场,磁感应强度大小为B,有一质量为m、带电量为+q的粒子从电场左边界与x轴的交点A沿x轴正方向射入电场区域,A点与坐标原点O的距离为x0,质点到达y轴上C点时,速度方向与y轴负方向之间的夹角为θ=30°.质点由C点进入磁场后,从磁场边界OM上的N点(图中未标出)离开磁场之后,又从y轴上的D点垂直于y轴进入电场,最后恰好回到A点.不计粒子的重力,求:
如图所示,在xOy平面内,直线PQ和y轴之间存在沿y轴负方向的匀强电场,在第四象限和第一象限的部分区域内存在垂直纸面向内的匀强磁场,磁感应强度大小为B,有一质量为m、带电量为+q的粒子从电场左边界与x轴的交点A沿x轴正方向射入电场区域,A点与坐标原点O的距离为x0,质点到达y轴上C点时,速度方向与y轴负方向之间的夹角为θ=30°.质点由C点进入磁场后,从磁场边界OM上的N点(图中未标出)离开磁场之后,又从y轴上的D点垂直于y轴进入电场,最后恰好回到A点.不计粒子的重力,求: 如图所示,圆形金属线框半径r=0.5m,圆形线框平面垂直于磁场方向放置,匀强磁场的磁感应强度B=1.0T,现把圆形线框翻转180°,所用时间△t=0.2s,则这段时间内线圈中产生的感应电动势为7.85V.
如图所示,圆形金属线框半径r=0.5m,圆形线框平面垂直于磁场方向放置,匀强磁场的磁感应强度B=1.0T,现把圆形线框翻转180°,所用时间△t=0.2s,则这段时间内线圈中产生的感应电动势为7.85V.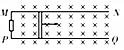 如图所示,两根足够长的平行粗糙的金属轨道MN、PQ固定在绝缘水平面内,相距为l,导轨左端与阻值为R的电阻相连.现有一质量为m、长也为l的金属棒,搁置在两根金属导轨上,与导轨垂直且接触良好,整个装置处于竖直向下的匀强磁场中,磁感应强度大小为B,设磁场区域足够大,导轨足够长,导轨电阻和金属棒电阻不计,导轨与金属棒间的动摩擦因数为μ,重力加速度为g.
如图所示,两根足够长的平行粗糙的金属轨道MN、PQ固定在绝缘水平面内,相距为l,导轨左端与阻值为R的电阻相连.现有一质量为m、长也为l的金属棒,搁置在两根金属导轨上,与导轨垂直且接触良好,整个装置处于竖直向下的匀强磁场中,磁感应强度大小为B,设磁场区域足够大,导轨足够长,导轨电阻和金属棒电阻不计,导轨与金属棒间的动摩擦因数为μ,重力加速度为g.