题目内容
4.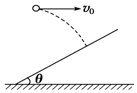 如图所示,以水平初速度v0抛出的小球,飞行一段时间后垂直地撞在倾角为θ的斜面上,则小球飞行的水平位移为( )
如图所示,以水平初速度v0抛出的小球,飞行一段时间后垂直地撞在倾角为θ的斜面上,则小球飞行的水平位移为( )| A. | $\frac{{{v}_{0}}^{2}}{g}$tanθ | B. | $\frac{{{v}_{0}}^{2}}{g}$cotθ | C. | $\frac{2{{v}_{0}}^{2}}{g}$tanθ | D. | $\frac{2{{v}_{0}}^{2}}{g}$cotθ |
分析 小球垂直地撞在倾角θ为30°的斜面上,知小球的速度方向与斜面垂直,将该速度进行分解,根据水平方向上的速度求出竖直方向上的分速度,根据分运动公式列式求解时间,由$x={v}_{0}^{\;}t$求出水平位移;
解答 解:小球撞在斜面上的速度与斜面垂直,将该速度分解,如图:
$tanθ=\frac{{v}_{0}^{\;}}{{v}_{y}^{\;}}=\frac{{v}_{0}^{\;}}{gt}$
解得:$t=\frac{{v}_{0}^{\;}}{gtanθ}$=$\frac{{v}_{0}^{\;}cotθ}{g}$
水平位移:$x={v}_{0}^{\;}t=\frac{{v}_{0}^{2}cotθ}{g}$
故选:B
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,根据竖直方向上的分速度规律求出运动的时间,基础题目.

练习册系列答案
相关题目
14. 如图所示为一个电池组和一只电阻R的U-I图线.用该电池组与电阻R直接R电阻连接成闭合电路,则以下说法正确的是( )
如图所示为一个电池组和一只电阻R的U-I图线.用该电池组与电阻R直接R电阻连接成闭合电路,则以下说法正确的是( )
 如图所示为一个电池组和一只电阻R的U-I图线.用该电池组与电阻R直接R电阻连接成闭合电路,则以下说法正确的是( )
如图所示为一个电池组和一只电阻R的U-I图线.用该电池组与电阻R直接R电阻连接成闭合电路,则以下说法正确的是( )| A. | 电池组的内阻是0.5Ω | |
| B. | 电阻的阻值为2Ω | |
| C. | 电池组的输出功率将是5W | |
| D. | 改变电阻R的阻值时,读电池组的最大输出功率为6.25W |
12. 如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设物体经过B点前后速度大小不变),最后停在C点.测得每隔2s的三个时刻物体的瞬时速度记录在表格中,由此可知( )
如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设物体经过B点前后速度大小不变),最后停在C点.测得每隔2s的三个时刻物体的瞬时速度记录在表格中,由此可知( )
 如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设物体经过B点前后速度大小不变),最后停在C点.测得每隔2s的三个时刻物体的瞬时速度记录在表格中,由此可知( )
如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设物体经过B点前后速度大小不变),最后停在C点.测得每隔2s的三个时刻物体的瞬时速度记录在表格中,由此可知( )| t/s | 0 | 2 | 4 | 6 |
| v/(m•s-1) | 0 | 8 | 12 | 8 |
| A. | 物体运动过程中的最大速度为12 m/s | |
| B. | t=3s的时刻物体恰好经过B点 | |
| C. | t=10s的时刻物体恰好停在C点 | |
| D. | A、B间的距离小于B、C间的距离 |
9.下列说法正确的是( )
| A. | 波动性和粒子性,在宏观现象中是矛盾的、对立的,但在微观高速度运动现象中是统一的 | |
| B. | 德布罗意波的正确性是康普顿利用康普顿效应证明的 | |
| C. | 让处于基态氢原子激发到激发态,所需的最小能量为10.2eV | |
| D. | 重核裂变成中等质量的核,核子平均结合能变大,平均质量变小 | |
| E. | 原子核的半衰期会受温度、压强、体积等因素影响 |
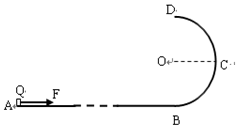 某游乐场中一种玩具车的运动情况可以简化为如下模型:如图所示,轨道ABCD位于竖直平面内,水平轨道AB与竖直半圆轨道BCD相切于B点,C点与圆心O等高,质量m=10kg的小车Q(可视为质点)静止在水平轨道上的点A,已知A点与B点相距L=40m(图中AB之间的虚线表示未画完整的水平轨道),竖直圆轨道的半径R=3m,圆弧光滑;小车在水平轨道AB间运动时受到的阻力恒为其重力的0.25倍.其它摩擦与空气阻力均忽略不计.(g取10m/s2)
某游乐场中一种玩具车的运动情况可以简化为如下模型:如图所示,轨道ABCD位于竖直平面内,水平轨道AB与竖直半圆轨道BCD相切于B点,C点与圆心O等高,质量m=10kg的小车Q(可视为质点)静止在水平轨道上的点A,已知A点与B点相距L=40m(图中AB之间的虚线表示未画完整的水平轨道),竖直圆轨道的半径R=3m,圆弧光滑;小车在水平轨道AB间运动时受到的阻力恒为其重力的0.25倍.其它摩擦与空气阻力均忽略不计.(g取10m/s2) 如图所示,传送带Ⅰ与水平面夹角30°,传送带Ⅱ与水平面夹角37°,两传送带与一小段光滑的水平面BC平滑连接.两传送带均顺顺时针匀速率运行.现将装有货物的箱子轻放至传送带Ⅰ的A点,运送到水平面上后,工作人员将箱子内的物体取下,箱子速度不变继续运动到传送带Ⅱ上,传送带Ⅱ的D点与高处平台相切.已知箱子的质量M=1kg,物体的质量m=3kg,传送带Ⅰ的速度v1=8m/s,AB长L1=15m,与箱子间的动摩擦因数为μ1=$\frac{\sqrt{3}}{2}$.传送带Ⅱ速度v2=4m/s,CD长L2=8m,由于水平面BC上不小心撒上水,致使箱子与传送带Ⅱ间的动摩擦因数变为μ2=0.5,重力加速度g=10m/s2,求:
如图所示,传送带Ⅰ与水平面夹角30°,传送带Ⅱ与水平面夹角37°,两传送带与一小段光滑的水平面BC平滑连接.两传送带均顺顺时针匀速率运行.现将装有货物的箱子轻放至传送带Ⅰ的A点,运送到水平面上后,工作人员将箱子内的物体取下,箱子速度不变继续运动到传送带Ⅱ上,传送带Ⅱ的D点与高处平台相切.已知箱子的质量M=1kg,物体的质量m=3kg,传送带Ⅰ的速度v1=8m/s,AB长L1=15m,与箱子间的动摩擦因数为μ1=$\frac{\sqrt{3}}{2}$.传送带Ⅱ速度v2=4m/s,CD长L2=8m,由于水平面BC上不小心撒上水,致使箱子与传送带Ⅱ间的动摩擦因数变为μ2=0.5,重力加速度g=10m/s2,求: 如图所示,在竖直平面内有一个正交的匀强电场和匀强磁场,磁感应强度为4T,电场强度为10$\sqrt{3}$N/C,一个带正电的微粒,q=2×10-6C,质量m=2×10-6kg,在这正交的电场的磁场内恰好做匀速直线运动,g=10m/s2,求:
如图所示,在竖直平面内有一个正交的匀强电场和匀强磁场,磁感应强度为4T,电场强度为10$\sqrt{3}$N/C,一个带正电的微粒,q=2×10-6C,质量m=2×10-6kg,在这正交的电场的磁场内恰好做匀速直线运动,g=10m/s2,求: