题目内容
14. 如图所示,在竖直平面内有一个正交的匀强电场和匀强磁场,磁感应强度为4T,电场强度为10$\sqrt{3}$N/C,一个带正电的微粒,q=2×10-6C,质量m=2×10-6kg,在这正交的电场的磁场内恰好做匀速直线运动,g=10m/s2,求:
如图所示,在竖直平面内有一个正交的匀强电场和匀强磁场,磁感应强度为4T,电场强度为10$\sqrt{3}$N/C,一个带正电的微粒,q=2×10-6C,质量m=2×10-6kg,在这正交的电场的磁场内恰好做匀速直线运动,g=10m/s2,求:(1)带电粒子受到的洛伦兹力的大小
(2)带电粒子运动的速度大小
(3)带电粒子运动的速度方向.
分析 (1)粒子受重力、电场力和洛伦兹力,做匀速直线运动,故合力为零根据平衡条件并运用正交分解法列式求解洛仑兹力;
(2)根据f=qvB求解速度大小;
(3)根据左手定则判断洛仑兹力的方向.
解答  解:粒子在重力、电场力与磁场力作用下做匀速直线运动.粒子的受力如图所示.
解:粒子在重力、电场力与磁场力作用下做匀速直线运动.粒子的受力如图所示.
水平方向:qE=fcosα…①,
竖直方向:fsinα=mg…②,
其中:f=qvB…③,
联立①②③,解得:
f=4×10-5N,
v=5m/s
α=30°
答:(1)带电粒子受到的洛伦兹力的大小为4×10-5N;
(2)带电粒子运动的速度大小为5m/s;
(3)带电粒子运动的速度方向与水平方向成30°斜向左上方.
点评 本题关键是根据物体做匀速直线运动的条件,运用平衡条件进行列式计算,要注意粒子做直线运动的条件是合力为零或者合力与速度共线,如果是变速运动,洛仑兹力大小变化,合力方向不可能恒定,故有洛仑兹力的直线运动通常都是匀速直线运动.

练习册系列答案
相关题目
4.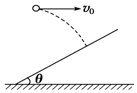 如图所示,以水平初速度v0抛出的小球,飞行一段时间后垂直地撞在倾角为θ的斜面上,则小球飞行的水平位移为( )
如图所示,以水平初速度v0抛出的小球,飞行一段时间后垂直地撞在倾角为θ的斜面上,则小球飞行的水平位移为( )
 如图所示,以水平初速度v0抛出的小球,飞行一段时间后垂直地撞在倾角为θ的斜面上,则小球飞行的水平位移为( )
如图所示,以水平初速度v0抛出的小球,飞行一段时间后垂直地撞在倾角为θ的斜面上,则小球飞行的水平位移为( )| A. | $\frac{{{v}_{0}}^{2}}{g}$tanθ | B. | $\frac{{{v}_{0}}^{2}}{g}$cotθ | C. | $\frac{2{{v}_{0}}^{2}}{g}$tanθ | D. | $\frac{2{{v}_{0}}^{2}}{g}$cotθ |
5.下列几组共点力分别作用在一个物体上,有可能使物体达到平衡状态的是( )
| A. | 7N,5N,3N | B. | 3N,4N,8N | C. | 4N,10N,5N | D. | 24N,8N,12N |
2.一个由静止开始做匀加速直线运动的物体,从开始运动起连续发生3段位移,在这3段位移中所用的时间分别是1s,2s,3s,这3段位移的大小之比和这3段位移上的平均速度之比分别为( )
| A. | 位移大小之比:1:22:32 | B. | 位移大小之比:1:23:33 | ||
| C. | 平均速度之比:1:22:32 | D. | 平均速度之比:1:2:3 |
19. 如图所示,斜面体A静置于粗糙水平面上,小球B置于光滑的斜面上,用一轻绳拴住B,轻绳左端固定在竖直墙面上P处.初始时轻绳与斜面平行,若将轻绳左端从P处缓慢沿墙面上移到P'处,斜面体始终处于静止状态,则在轻绳移动过程中( )
如图所示,斜面体A静置于粗糙水平面上,小球B置于光滑的斜面上,用一轻绳拴住B,轻绳左端固定在竖直墙面上P处.初始时轻绳与斜面平行,若将轻绳左端从P处缓慢沿墙面上移到P'处,斜面体始终处于静止状态,则在轻绳移动过程中( )
 如图所示,斜面体A静置于粗糙水平面上,小球B置于光滑的斜面上,用一轻绳拴住B,轻绳左端固定在竖直墙面上P处.初始时轻绳与斜面平行,若将轻绳左端从P处缓慢沿墙面上移到P'处,斜面体始终处于静止状态,则在轻绳移动过程中( )
如图所示,斜面体A静置于粗糙水平面上,小球B置于光滑的斜面上,用一轻绳拴住B,轻绳左端固定在竖直墙面上P处.初始时轻绳与斜面平行,若将轻绳左端从P处缓慢沿墙面上移到P'处,斜面体始终处于静止状态,则在轻绳移动过程中( )| A. | 轻绳的拉力逐渐减小 | B. | 斜面体对小球的支持力逐渐减小 | ||
| C. | 斜面体对水平面的压力逐渐增大 | D. | 斜面体对水平面的摩擦力逐渐减小 |
6. 如图所示,质量均为1kg的物体A、B相对静止向左a=3m/s2的匀加速运动,弹簧处于压缩状态,弹力为2N,则B对A的摩擦力为( )
如图所示,质量均为1kg的物体A、B相对静止向左a=3m/s2的匀加速运动,弹簧处于压缩状态,弹力为2N,则B对A的摩擦力为( )
 如图所示,质量均为1kg的物体A、B相对静止向左a=3m/s2的匀加速运动,弹簧处于压缩状态,弹力为2N,则B对A的摩擦力为( )
如图所示,质量均为1kg的物体A、B相对静止向左a=3m/s2的匀加速运动,弹簧处于压缩状态,弹力为2N,则B对A的摩擦力为( )| A. | 0 | B. | 向左1N | C. | 向右1N | D. | 向左3N |
4.刚刚学习了功率的四个公式:①P=UI;②P=I2R;③P=$\frac{{U}^{2}}{R}$;④P=$\frac{W}{t}$,下列叙述中正确的是( )
| A. | 公式①④适用于任何电路的电功率的计算 | |
| B. | 公式②适用于任何电路的电热功率的计算 | |
| C. | 公式①②③适用于任何电路的电功率的计算 | |
| D. | 由公式④可知:功率P与电流做的功W成正比,与时间t成反比 |
 在如图所示的装置中,平台的AB段粗糙,且长度为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均光滑,且BC的始、末端均水平,具有h=0.1m的高度差,DEN是半径为r=0.4m固定于地面上的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让物体自由通过.在左端竖直墙上固定有一轻质弹簧,现有一可视为质点的小物块,小物块质量m=0.2kg,压缩轻质弹簧至A点后由静止释放(小物块和弹簧不粘连),小物块刚好能沿DEN轨道滑下.(g=10m/s2)求:
在如图所示的装置中,平台的AB段粗糙,且长度为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均光滑,且BC的始、末端均水平,具有h=0.1m的高度差,DEN是半径为r=0.4m固定于地面上的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让物体自由通过.在左端竖直墙上固定有一轻质弹簧,现有一可视为质点的小物块,小物块质量m=0.2kg,压缩轻质弹簧至A点后由静止释放(小物块和弹簧不粘连),小物块刚好能沿DEN轨道滑下.(g=10m/s2)求: