题目内容
15.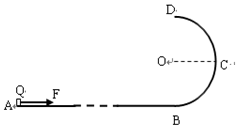 某游乐场中一种玩具车的运动情况可以简化为如下模型:如图所示,轨道ABCD位于竖直平面内,水平轨道AB与竖直半圆轨道BCD相切于B点,C点与圆心O等高,质量m=10kg的小车Q(可视为质点)静止在水平轨道上的点A,已知A点与B点相距L=40m(图中AB之间的虚线表示未画完整的水平轨道),竖直圆轨道的半径R=3m,圆弧光滑;小车在水平轨道AB间运动时受到的阻力恒为其重力的0.25倍.其它摩擦与空气阻力均忽略不计.(g取10m/s2)
某游乐场中一种玩具车的运动情况可以简化为如下模型:如图所示,轨道ABCD位于竖直平面内,水平轨道AB与竖直半圆轨道BCD相切于B点,C点与圆心O等高,质量m=10kg的小车Q(可视为质点)静止在水平轨道上的点A,已知A点与B点相距L=40m(图中AB之间的虚线表示未画完整的水平轨道),竖直圆轨道的半径R=3m,圆弧光滑;小车在水平轨道AB间运动时受到的阻力恒为其重力的0.25倍.其它摩擦与空气阻力均忽略不计.(g取10m/s2)(1)若小车在水平轨道上运动时受到水平向右的恒力F的作用,使小车恰好能到达半圆轨道的C点,求恒力F的大小.
(2)若小车在适当的拉力作用下,恰好能到达竖直半圆轨道的最高点D,求小车经过半圆轨道B点时受到的支持力大小.
(3)若小车用自带的电动机提供动力,电动机输出功率恒为P=50W,要使小车不脱离轨道,求发动机工作时间t需满足的条件(设经过所求的时间,小车还没到B点).
分析 (1)对于AC过程,运用动能定理列式,可求得F的大小.
(2)小车恰好能到达竖直半圆轨道的最高点D,在D点,由重力提供向心力,根据牛顿第二定律可求得D点的速度.B到D过程,由机械能守恒定律求出小车通过B点的速度.再由牛顿第二定律求小车经过半圆轨道B点时受到的支持力大小.
(3)小车不脱离轨道有两种情况:一是小车上升的高度不超过C点.二是能通过最高点D,根据临界条件和动能定理结合解答.
解答 解:(1)从A到C,由动能定理可得:
FL-μmgL-mgR=0-0
代入数据解得:F=32.5N
(2)小车恰好能到达竖直半圆轨道的最高点D,在D点,由重力提供向心力,根据牛顿第二定律得:
mg=m$\frac{{v}_{2}^{2}}{R}$
小车由B点运动到D点的过程中,由机械能守恒定律得:
$\frac{1}{2}m{v}_{1}^{2}$=2mgR+$\frac{1}{2}m{v}_{2}^{2}$
解得:v1=$\sqrt{5gR}$
小车经过半圆轨道B点时,由牛顿第二定律得:
F-mg=m$\frac{{v}_{1}^{2}}{R}$
代入数据解得:F=600N
(3)小车不脱离轨道情景一:小车上升的高度不超过C点.
临界情况,小车恰好到达C点.
AC过程列动能定理得:Pt1-μmgL-mgR=0-0
代入数据得:t1=26s
不脱离轨道情景二:小车能上升到最高点D,临界情况需满足:
mg=m$\frac{{v}_{D}^{2}}{R}$
A到D过程列动能定理得:
Pt2-μmgL-mg•2R=$\frac{1}{2}$mvD2.
解得 t2=35s
所以发动机工作时间t需满足的条件是t1≤26s或者t2≥35s.
答:(1)恒力F的大小为32.5N.
(2)小车经过半圆轨道B点时受到的支持力大小是600N.
(3)发动机工作时间t需满足的条件是t1≤26s或者t2≥35s.
点评 本题主要考查了动能定理,在第三问中,抓住沿轨道运动:不能到达最高点,在C点下方速度减到零,或者到达最高点做圆周运动,再结合动能定理即可研究.

 快捷英语周周练系列答案
快捷英语周周练系列答案| 初始速度(m/s) | 经过时间(s) | 末速度(m/s) | |
| ① | 2 | 3 | 11 |
| ② | 0 | 3 | 6 |
| ③ | 0 | 20 | 6 |
| ④ | 0 | 100 | 20 |
| A. | ①的速度变化最大,加速度最大 | B. | ②的速度变化最小 | ||
| C. | ③的速度变化最快 | D. | ④的末速度最大,但加速度最小 |
 2016年里约奥运会上,体操比赛吊环项目中有一个高难度的动作就是先双手撑住吊环,然后身体下移,双臂缓慢张开到如图所示位置,则在两手之间的距离缓慢增大的过程中,吊环的两根绳的拉力FT(两个拉力大小相等)及它们的合力F 的大小变化情况为( )
2016年里约奥运会上,体操比赛吊环项目中有一个高难度的动作就是先双手撑住吊环,然后身体下移,双臂缓慢张开到如图所示位置,则在两手之间的距离缓慢增大的过程中,吊环的两根绳的拉力FT(两个拉力大小相等)及它们的合力F 的大小变化情况为( )| A. | FT增大,F减小 | B. | FT增大,F增大 | C. | FT增大,F不变 | D. | FT减小,F不变 |
| A. | 40 N | B. | 70 N | C. | 100 N | D. | 6 N |

| A. | 甲是晶体,乙、丙是非晶体 | B. | 乙是晶体,甲、丙是非晶体 | ||
| C. | 乙是非晶体,甲的熔点比丙低 | D. | 乙是非晶体,甲的熔点比丙高 |

| A. | 当r大于r1时,分子间的作用力表现为引力 | |
| B. | 当r等于r2时,分子间的作用力表现为斥力 | |
| C. | 当r小于r1时,分子间的作用力表现为斥力 | |
| D. | 在r由r1变到r2的过程中,分子间的作用力做负功 |
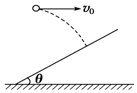 如图所示,以水平初速度v0抛出的小球,飞行一段时间后垂直地撞在倾角为θ的斜面上,则小球飞行的水平位移为( )
如图所示,以水平初速度v0抛出的小球,飞行一段时间后垂直地撞在倾角为θ的斜面上,则小球飞行的水平位移为( )| A. | $\frac{{{v}_{0}}^{2}}{g}$tanθ | B. | $\frac{{{v}_{0}}^{2}}{g}$cotθ | C. | $\frac{2{{v}_{0}}^{2}}{g}$tanθ | D. | $\frac{2{{v}_{0}}^{2}}{g}$cotθ |
| A. | 7N,5N,3N | B. | 3N,4N,8N | C. | 4N,10N,5N | D. | 24N,8N,12N |