题目内容
7.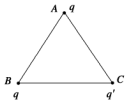 如图所示,在等边三角形ABC的三个顶点上,固定三个正点电荷,电荷量的大小q′<q,则三角形ABC的几何中心处电场强度的方向( )
如图所示,在等边三角形ABC的三个顶点上,固定三个正点电荷,电荷量的大小q′<q,则三角形ABC的几何中心处电场强度的方向( )| A. | 平行于AC边 | B. | 平行于AB边 | C. | 垂直于AB边指向C | D. | 垂直于AC边指向B |
分析 三角形ABC的几何中心到三角形三个顶点的距离相等,根据点电荷场强公式E=k$\frac{Q}{{r}^{2}}$和平行四边形定则分析两个点电荷q在中心处产生的合场强大小和方向,与q′在中心处产生的场强大小和方向进行比较,确定三角形ABC的几何中心处电场强度的方向.
解答 解:根据几何知识得知,三角形ABC的几何中心到三角形三个顶点的距离相等,设为r.由点电荷场强公式E=k$\frac{Q}{{r}^{2}}$可知,两个点电荷q在中心处产生的场强大小均为E1=k$\frac{q}{{r}^{2}}$,两个场强之间的夹角为120°,根据平行四边形定则得到:两个点电荷q在中心处产生的合场强大小 E合=E1=k$\frac{q}{{r}^{2}}$,方向沿垂直于AB边指向C.
q′在中心处产生的场强大小为E2=k$\frac{q′}{{r}^{2}}$,方向沿垂直于AB边离开C.由于q′<q,则E合>E2,所以三角形ABC的几何中心处电场强度的方向沿垂直于AB边指向C.故ABD错误,C正确
故选:C
点评 本题是电场的叠加问题,要在掌握点电荷场强公式E=k$\frac{Q}{{r}^{2}}$的基础上,运用平行四边形定则进行合成.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17. 有一人造卫星正从近地轨道1向高轨道3跃迁.在近地点A处点火加速后,沿椭圆形轨道向远地点B运行,在远地点B处点火加速后,进入高轨道3.正确的有( )
有一人造卫星正从近地轨道1向高轨道3跃迁.在近地点A处点火加速后,沿椭圆形轨道向远地点B运行,在远地点B处点火加速后,进入高轨道3.正确的有( )
 有一人造卫星正从近地轨道1向高轨道3跃迁.在近地点A处点火加速后,沿椭圆形轨道向远地点B运行,在远地点B处点火加速后,进入高轨道3.正确的有( )
有一人造卫星正从近地轨道1向高轨道3跃迁.在近地点A处点火加速后,沿椭圆形轨道向远地点B运行,在远地点B处点火加速后,进入高轨道3.正确的有( )| A. | 卫星从A到B的过程,万有引力做负功,引力势能增加 | |
| B. | 卫星从A到B的过程,机械能不变,万有引力也不做功 | |
| C. | 卫星在由轨道1向轨道2转移的两轨道切点A处动能不变 | |
| D. | 同一卫星在1、3两轨道相比,1处的动能大、机械能小 |
18.静止在地球表面跟随地球自转的物体,受到的作用力有( )
| A. | 引力,重力,弹力 | B. | 引力,弹力 | ||
| C. | 引力,向心力,弹力 | D. | 引力,向心力,弹力,重力 |
15.硅光电池是利用光电效应原理制成的器件,下列表述正确的是( )
| A. | 硅光电池是把光能转变为电能的一种装置 | |
| B. | 硅光电池中吸收了光子能量的电子都能逸出 | |
| C. | 入射光的光强越强,则逸出的光电子最大初始动能就越大 | |
| D. | 任意频率的光照射到硅光电池上都能产生光电效应 |
4. 如图所示,一倾角为a的固定斜面下端固定一挡板,一劲度系数为k的轻弹簧下端固定在挡板上.现将一质量为m的小物块从斜面上离弹簧上端距离为s处,由静止释放,已知物块与斜面间的动摩擦因数为μ,物块下滑过程中的最大动能为Ekm,则小物块从释放到运动至最低点的过程中,下列说法中正确的是( )
如图所示,一倾角为a的固定斜面下端固定一挡板,一劲度系数为k的轻弹簧下端固定在挡板上.现将一质量为m的小物块从斜面上离弹簧上端距离为s处,由静止释放,已知物块与斜面间的动摩擦因数为μ,物块下滑过程中的最大动能为Ekm,则小物块从释放到运动至最低点的过程中,下列说法中正确的是( )
 如图所示,一倾角为a的固定斜面下端固定一挡板,一劲度系数为k的轻弹簧下端固定在挡板上.现将一质量为m的小物块从斜面上离弹簧上端距离为s处,由静止释放,已知物块与斜面间的动摩擦因数为μ,物块下滑过程中的最大动能为Ekm,则小物块从释放到运动至最低点的过程中,下列说法中正确的是( )
如图所示,一倾角为a的固定斜面下端固定一挡板,一劲度系数为k的轻弹簧下端固定在挡板上.现将一质量为m的小物块从斜面上离弹簧上端距离为s处,由静止释放,已知物块与斜面间的动摩擦因数为μ,物块下滑过程中的最大动能为Ekm,则小物块从释放到运动至最低点的过程中,下列说法中正确的是( )| A. | μ<tana | |
| B. | 物块刚与弹簧接触的瞬间达到最大动能 | |
| C. | 弹簧的最大弹性势能等于整个过程中物块减少的重力势能与摩擦力对物块做功之和 | |
| D. | 若将物块从离弹簧上端2s的斜面处由静止释放,则下滑过程中物块的最大动能小于2Ekm |
11. 如图所示,质量为M的木块静止在光滑水平面上,质量为m的子弹以水平速度v0射入木块,并留在木块里.已知在子弹射入木块的过程中子弹发生的位移为x1,木块发生的位移为x2,子弹进入木块深度为x,子弹受到阻力大小恒为Ff,子弹射入木块后二者的共同速度为vt,不计空气阻力影响,下列结论中正确的是( )
如图所示,质量为M的木块静止在光滑水平面上,质量为m的子弹以水平速度v0射入木块,并留在木块里.已知在子弹射入木块的过程中子弹发生的位移为x1,木块发生的位移为x2,子弹进入木块深度为x,子弹受到阻力大小恒为Ff,子弹射入木块后二者的共同速度为vt,不计空气阻力影响,下列结论中正确的是( )
 如图所示,质量为M的木块静止在光滑水平面上,质量为m的子弹以水平速度v0射入木块,并留在木块里.已知在子弹射入木块的过程中子弹发生的位移为x1,木块发生的位移为x2,子弹进入木块深度为x,子弹受到阻力大小恒为Ff,子弹射入木块后二者的共同速度为vt,不计空气阻力影响,下列结论中正确的是( )
如图所示,质量为M的木块静止在光滑水平面上,质量为m的子弹以水平速度v0射入木块,并留在木块里.已知在子弹射入木块的过程中子弹发生的位移为x1,木块发生的位移为x2,子弹进入木块深度为x,子弹受到阻力大小恒为Ff,子弹射入木块后二者的共同速度为vt,不计空气阻力影响,下列结论中正确的是( )| A. | Ffx=$\frac{mv_0^2}{2}-\frac{{M{v_t}^2}}{2}$ | B. | Ffx1=$\frac{mv_0^2}{2}-\frac{{m{v_t}^2}}{2}$ | ||
| C. | Ffx2=$\frac{{M{v_t}^2}}{2}$ | D. | Ffx=$\frac{mv_0^2}{2}-\frac{{(m+M){v_t}^2}}{2}$ |
9.互联网正在极大地促进商业的发展和消费的升级,“020”模式是指将线下的商务机会与互联网结合,让互联网成为线下交易的前台的一种商业新模式,具体到一家外卖公司与消费之间,就是消费者在网络平台上下单订购,而公司进行线下的配送服务.某外卖公司为了更好地为消费者服务,配送员工使用的是“XR一 2016”型电动自行车工作,以下是该车的相关参数:
该电动自行车采用后轮驱动直流电动机,其中额定转速是电动自行车在满载情况下在平直公路 上以额定功率勻速行进时的车轮转速,求:
(1)电动自行车以额定转速行进时的速度v0;在额定工作状态时,损失的功率有80%是由于 电动机绕线电阻生热而产生的,则电动机的绕线电阻为多大;
(2)满载(车身质量+满载载重质量)情况下,该车以速度v=5m/s沿着坡度为θ=4.59°的长直坡道向上匀速行驶时,受到的摩擦阻力为车重(含载重)重量的0.02倍,求此状态下电动自行车实际运行机械功率(sin4.59°=0.08,重力加速度g=10m/s2).
| 名称 | 车身质量 | 满载载重 | 前后车轮直径 | 额定转速 | 电动机额定电压 | 电动机额定电流 | 额定机械输出功率 |
| 参数 | 40kg | 80kg | 40cm | r/min | 48V | 20A | 835W |
(1)电动自行车以额定转速行进时的速度v0;在额定工作状态时,损失的功率有80%是由于 电动机绕线电阻生热而产生的,则电动机的绕线电阻为多大;
(2)满载(车身质量+满载载重质量)情况下,该车以速度v=5m/s沿着坡度为θ=4.59°的长直坡道向上匀速行驶时,受到的摩擦阻力为车重(含载重)重量的0.02倍,求此状态下电动自行车实际运行机械功率(sin4.59°=0.08,重力加速度g=10m/s2).