题目内容
11. 如图所示,质量为M的木块静止在光滑水平面上,质量为m的子弹以水平速度v0射入木块,并留在木块里.已知在子弹射入木块的过程中子弹发生的位移为x1,木块发生的位移为x2,子弹进入木块深度为x,子弹受到阻力大小恒为Ff,子弹射入木块后二者的共同速度为vt,不计空气阻力影响,下列结论中正确的是( )
如图所示,质量为M的木块静止在光滑水平面上,质量为m的子弹以水平速度v0射入木块,并留在木块里.已知在子弹射入木块的过程中子弹发生的位移为x1,木块发生的位移为x2,子弹进入木块深度为x,子弹受到阻力大小恒为Ff,子弹射入木块后二者的共同速度为vt,不计空气阻力影响,下列结论中正确的是( )| A. | Ffx=$\frac{mv_0^2}{2}-\frac{{M{v_t}^2}}{2}$ | B. | Ffx1=$\frac{mv_0^2}{2}-\frac{{m{v_t}^2}}{2}$ | ||
| C. | Ffx2=$\frac{{M{v_t}^2}}{2}$ | D. | Ffx=$\frac{mv_0^2}{2}-\frac{{(m+M){v_t}^2}}{2}$ |
分析 子弹射入木块的过程中,木块对子弹的阻力f做功为-Ffx1,子弹对木块的作用力做功为Ffx2,根据动能定理,分别以木块和子弹为研究对象,分析子弹和木块的作用力做功与动能变化的关系.
解答 解:以子弹为研究对象,由动能定理得:-Ffx1=$\frac{1}{2}m{v}_{t}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$…①
则得:Ffx1=$\frac{mv_0^2}{2}-\frac{{m{v_t}^2}}{2}$.
以木块为研究对象,根据动能定理得,子弹对木块做功等于木块动能的增加,即 Ffx2=$\frac{{M{v_t}^2}}{2}$…②.
因为 x=x1-x2,由①+②得,-Ffx=$\frac{1}{2}$(M+m)${v}_{t}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$,则得 Ffx=$\frac{1}{2}m{v}_{0}^{2}$-$\frac{1}{2}$(M+m)${v}_{t}^{2}$…③,故A错误,BCD正确.
故选:BCD
点评 本题是冲击块类型,要注意应用动能定理研究单个物体时,功的公式W=Fl中,l是相对于地的位移大小.D项,也可以根据能量守恒定律得到.

练习册系列答案
相关题目
9.汽车启动后以额定功率在粗糙的水平公路上运动,下列说法中正确的是( )
| A. | 汽车速率达到最大值之前,加速度是不断增大的 | |
| B. | 汽车速率达到最大值之前,牵引力是不断减小的 | |
| C. | 汽车速率达到最大值之前,汽车做匀加速运动 | |
| D. | 如果路面越粗糙,阻力越大,汽车获得的最终速度也越小 |
10.2016年2月11日,美国“激光干涉引力波天文台”(LIGO)团队向全世界宣布发现了引力波,这个引力波来自于距离地球13亿光年之外一个双黑洞系统的合并.若某黑洞的半径R约为4.5km,黑洞质量M和半径R的关系满足$\frac{M}{R}$=$\frac{{c}^{2}}{2G}$(其中c为光速,G为引力常量),则该黑洞表面重力加速度的数量级为( )
| A. | 1011 m/s2 | B. | 1012 m/s2 | C. | 1013 m/s2 | D. | 1014 m/s2 |
7.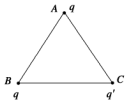 如图所示,在等边三角形ABC的三个顶点上,固定三个正点电荷,电荷量的大小q′<q,则三角形ABC的几何中心处电场强度的方向( )
如图所示,在等边三角形ABC的三个顶点上,固定三个正点电荷,电荷量的大小q′<q,则三角形ABC的几何中心处电场强度的方向( )
 如图所示,在等边三角形ABC的三个顶点上,固定三个正点电荷,电荷量的大小q′<q,则三角形ABC的几何中心处电场强度的方向( )
如图所示,在等边三角形ABC的三个顶点上,固定三个正点电荷,电荷量的大小q′<q,则三角形ABC的几何中心处电场强度的方向( )| A. | 平行于AC边 | B. | 平行于AB边 | C. | 垂直于AB边指向C | D. | 垂直于AC边指向B |
6.在做“用单摆测定重力加速度”的实验时,用摆长l和周期T计算重力加速度的公式是g=$\frac{{4{π^2}l}}{T^2}$.
(1)如果已知摆球直径为2.00cm,让刻度尺的零点对准摆线的悬点,摆线竖直下垂,如图(甲)所示,那么单摆摆长是87.50m,如果测定了40次全振动的时间如图(乙)中停表所示,那么停表读数是75.2S.单摆的振动周期是1.88s.

(2)如果测得的g值偏小,可能的原因是ABC(填写代号)
A.测摆长时,忘记了摆球的半径
B.摆线上端悬点未固定,振动中出现松动,使摆线长度增加了
C.开始计时时,停表过早按下
D.实验中误将40次全振动次数记为41次
(3)某同学在实验中,测量6种不同摆长情况下单摆的振动周期,记录表格如下;
以l为横坐标、T2为纵坐标,作出T2-l图线,并利用此图线求重力加速度g.
(1)如果已知摆球直径为2.00cm,让刻度尺的零点对准摆线的悬点,摆线竖直下垂,如图(甲)所示,那么单摆摆长是87.50m,如果测定了40次全振动的时间如图(乙)中停表所示,那么停表读数是75.2S.单摆的振动周期是1.88s.

(2)如果测得的g值偏小,可能的原因是ABC(填写代号)
A.测摆长时,忘记了摆球的半径
B.摆线上端悬点未固定,振动中出现松动,使摆线长度增加了
C.开始计时时,停表过早按下
D.实验中误将40次全振动次数记为41次
(3)某同学在实验中,测量6种不同摆长情况下单摆的振动周期,记录表格如下;
| l/m | 0.4 | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| T/s | 1.26 | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2/s2 | 1.59 | 2.02 | 3.20 | 3.61 | 4.0 | 4.84 |
16.如图甲所示,质量不计的弹簧竖直 固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( ) 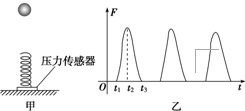

| A. | t1时刻小球动能最大 | |
| B. | t2时刻小球动能为0 | |
| C. | t2~t3这段时间内,小球的动能先减小后增加 | |
| D. | t2~t3这段时间内,小球增加的动能和重力势能之和等于弹簧减少的弹性势能 |
3.在电磁学发展的过程中,物理学家们所做的工作使得人们对电与磁内在联系的认识更加完善,下列叙述不符合史实的是( )
| A. | 法拉第在实验中观察到,静止导线上的稳恒电流可在近旁静止的线圈中感应出电流 | |
| B. | 楞次在分析了许多实验事实后提出:感应电流具有这样的方向,即感应电流的磁场总要阻碍引起感应电流的磁通量的变化 | |
| C. | 纽曼、韦伯在对理论和实验资料严格分析后先后指出:闭合电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比 | |
| D. | 麦克斯韦认为磁场变化时会在空间激发一种电场,这种电场是与静电场性质不同的场 |
1. 功和功率的计算)如图所示,一质量为1.2kg的物体从倾角为30°、长度为10m的光滑斜面顶端由静止开始下滑.则( )
功和功率的计算)如图所示,一质量为1.2kg的物体从倾角为30°、长度为10m的光滑斜面顶端由静止开始下滑.则( )
 功和功率的计算)如图所示,一质量为1.2kg的物体从倾角为30°、长度为10m的光滑斜面顶端由静止开始下滑.则( )
功和功率的计算)如图所示,一质量为1.2kg的物体从倾角为30°、长度为10m的光滑斜面顶端由静止开始下滑.则( )| A. | 物体滑到斜面底端时重力做功的瞬时功率是60W | |
| B. | 物体滑到斜面底端时重力做功的瞬时功率是120W | |
| C. | 整个过程中重力做功的平均功率是30W | |
| D. | 整个过程中重力做功的平均功率是60W |
 在如图所示p-V图象中,一定质量的理想气体从状态M变化至状态N,分别经历了过程1和过程2,已知M、N状态的温度相等,则在过程1中气体温度的变化情况是先变大再变小(选填“先减少后增大”、“不变”或“先增大后减少”),若过程1中气体吸热Q1,过程2中气体吸热Q2,则Q1>Q2(选填“>”、“=”或“<”).
在如图所示p-V图象中,一定质量的理想气体从状态M变化至状态N,分别经历了过程1和过程2,已知M、N状态的温度相等,则在过程1中气体温度的变化情况是先变大再变小(选填“先减少后增大”、“不变”或“先增大后减少”),若过程1中气体吸热Q1,过程2中气体吸热Q2,则Q1>Q2(选填“>”、“=”或“<”).