题目内容
19. 质点S在竖直方向做简谐运动,形成简谐横波水平向右传播,P、Q是波上两点,如图所示,从质点S起振开始计时,当S第5次到达上方振幅位置时,质点P刚开始向下起振.已知SP=1.9m,SQ=2.5m,质点S做简谐运动的频率为100Hz,振幅为0.2m,以质点S所在位置为坐标原点,SP方向为x轴,建立直角坐标,则( )
质点S在竖直方向做简谐运动,形成简谐横波水平向右传播,P、Q是波上两点,如图所示,从质点S起振开始计时,当S第5次到达上方振幅位置时,质点P刚开始向下起振.已知SP=1.9m,SQ=2.5m,质点S做简谐运动的频率为100Hz,振幅为0.2m,以质点S所在位置为坐标原点,SP方向为x轴,建立直角坐标,则( )| A. | 该波的传播速度为38m/s | |
| B. | 该波的波长为0.5m | |
| C. | 在t=0.08s时,质点Q已经运动的路程为1.4m | |
| D. | 在t=0.08s时,质点P、Q之间2.1m<x<2.3m的质点向下 |
分析 质点P刚开始向下起振,说明起振方向向下,求出根据S第5次到达上方振幅位置时所需要的时间,再根据v=$\frac{s}{t}$求解波速,波长λ=vT,求出在t=0.08s时,质点Q振动的时间,再根据一个周期内质点通过的路程为4A求解质点Q已经运动的路程.
解答 解:A、质点P刚开始向下起振,说明起振方向向下,S第5次到达上方振幅位置时所需要的时间t=$4\frac{3}{4}T=\frac{19}{4}×\frac{1}{100}=0.0475s$,
则波速v=$\frac{SP}{t}=\frac{1.9}{0.0475}=40m/s$,波长λ=vT=40×0.01=0.4m,故AB错误;
C、振动传到Q点的时间t$′=\frac{SQ}{v}=\frac{2.5}{40}=0.0625s$
在t=0.08s时,质点Q已经振动的时间t1=0.08-0.0625=0.0175s=1$\frac{3}{4}T$,运动的路程为s=$1\frac{3}{4}$×4A=$\frac{7}{4}$×4×0.2=1.4m,故C正确;
D、在t=0.08s时,质点Q处于波峰处,P点处于波谷处,质点P、Q之间2.1m<x<2.3m的质点向上振动,故D错误.
故选:C
点评 本题要把握住质点的振动过程与波动形成过程之间的联系,能根据S第5次到达上方振幅位置时所需要的时间,从而求出波速,打开突破口,难度适中.

练习册系列答案
相关题目
14.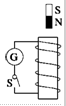 如图所示,闭合开关S,将条形磁铁两次插入闭合线圈,第一次用0.2s,第二次用0.4s,并且两次的起始和终止位置相同,则( )
如图所示,闭合开关S,将条形磁铁两次插入闭合线圈,第一次用0.2s,第二次用0.4s,并且两次的起始和终止位置相同,则( )
 如图所示,闭合开关S,将条形磁铁两次插入闭合线圈,第一次用0.2s,第二次用0.4s,并且两次的起始和终止位置相同,则( )
如图所示,闭合开关S,将条形磁铁两次插入闭合线圈,第一次用0.2s,第二次用0.4s,并且两次的起始和终止位置相同,则( )| A. | 第一次磁通量变化较大 | |
| B. | 第一次 的最大偏角较大 的最大偏角较大 | |
| C. | 第一次经过 的总电量较多 的总电量较多 | |
| D. | 若断开开关S, 均不偏转,故均无感应电动势 均不偏转,故均无感应电动势 |
4. 如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平速度v0射入木块,若子弹在木块中做匀减速直线运动,当穿透第三个木块时速度恰好为零,则子弹依次射入每个木块时的速度v1、v2、v3之比和穿过每个木块所用的时间t1、t2、t3之比分别为( )
如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平速度v0射入木块,若子弹在木块中做匀减速直线运动,当穿透第三个木块时速度恰好为零,则子弹依次射入每个木块时的速度v1、v2、v3之比和穿过每个木块所用的时间t1、t2、t3之比分别为( )
 如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平速度v0射入木块,若子弹在木块中做匀减速直线运动,当穿透第三个木块时速度恰好为零,则子弹依次射入每个木块时的速度v1、v2、v3之比和穿过每个木块所用的时间t1、t2、t3之比分别为( )
如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平速度v0射入木块,若子弹在木块中做匀减速直线运动,当穿透第三个木块时速度恰好为零,则子弹依次射入每个木块时的速度v1、v2、v3之比和穿过每个木块所用的时间t1、t2、t3之比分别为( )| A. | v1:v2:v3=1:2:3 | B. | v1:v2:v3=$\sqrt{3}:\sqrt{2}$:1 | ||
| C. | t1:t2:t3=1:$\sqrt{2}:\sqrt{3}$ | D. | t1:t2:t3=($\sqrt{3}$-$\sqrt{2}$):($\sqrt{2}$-1):1 |
 质量为m的通电细杆ab置于倾角为θ的平行导轨上,导轨宽为d,杆与导轨间的摩擦因数为μ,有电流时ab恰好在导轨上静止,如图所示.下图是从右侧观察时的四种不同的匀强磁场方向下的四个平面图,其中通电细杆ab与导轨间的摩擦力不可能为零的是( )
质量为m的通电细杆ab置于倾角为θ的平行导轨上,导轨宽为d,杆与导轨间的摩擦因数为μ,有电流时ab恰好在导轨上静止,如图所示.下图是从右侧观察时的四种不同的匀强磁场方向下的四个平面图,其中通电细杆ab与导轨间的摩擦力不可能为零的是( )



 滑雪是一项惊险又刺激的运动.某滑雪场的滑道如图所示,AB为倾角θ=37°的斜滑道,BC为高h=0.8m的竖直山坡,CD为水平滑道.有一滑雪者从A点由静止滑下.到B点经一小段不计长度的圆弧后水平滑出,落在了水平滑道的D点,已知滑雪板与滑道间的动摩擦因数μ=0.15,落点D与C之间的距离为9.6m.不计空气阻力,g=10m/s2,sin37°=0.6,cos37°=0.8.求:
滑雪是一项惊险又刺激的运动.某滑雪场的滑道如图所示,AB为倾角θ=37°的斜滑道,BC为高h=0.8m的竖直山坡,CD为水平滑道.有一滑雪者从A点由静止滑下.到B点经一小段不计长度的圆弧后水平滑出,落在了水平滑道的D点,已知滑雪板与滑道间的动摩擦因数μ=0.15,落点D与C之间的距离为9.6m.不计空气阻力,g=10m/s2,sin37°=0.6,cos37°=0.8.求: 如图所示,质量均为m的小车与木箱紧挨着静止在光滑的水平冰面上,质量为2m的小明站在小车上用力向右迅速推出木箱后,木箱相对于冰面的速度为v,接着木箱与右侧竖直墙壁发生弹性碰撞,反弹后被小明接住,求
如图所示,质量均为m的小车与木箱紧挨着静止在光滑的水平冰面上,质量为2m的小明站在小车上用力向右迅速推出木箱后,木箱相对于冰面的速度为v,接着木箱与右侧竖直墙壁发生弹性碰撞,反弹后被小明接住,求 一质量为m的滑块(视为质点),从水平面上与一平面相切与A点以V0=$\sqrt{8Rg}$的速度进入竖直半圆形轨道开始作圆周运动,轨道半径为R,经半圆轨道的最高点B飞出,落回到水平面上的C点,如图所示,若AC=2AB=4R
一质量为m的滑块(视为质点),从水平面上与一平面相切与A点以V0=$\sqrt{8Rg}$的速度进入竖直半圆形轨道开始作圆周运动,轨道半径为R,经半圆轨道的最高点B飞出,落回到水平面上的C点,如图所示,若AC=2AB=4R 如图所示,在竖直平面内,粗糙的斜面轨道AB的下端与光滑的圆弧轨道BCD相切于B点,C是最低点,圆心角∠BOC=37°,D与圆心O等高,圆弧轨道半径R=1.0m,现有一个质量为m=0.2kg可视为质点的小物体,从D点的正上方E点处自由下落,DE距离h=1.6m,物体与斜面AB之间的动摩擦因数μ=0.5.取sin37°=0.6,cos37°=0.8,g=10m/s2.求:
如图所示,在竖直平面内,粗糙的斜面轨道AB的下端与光滑的圆弧轨道BCD相切于B点,C是最低点,圆心角∠BOC=37°,D与圆心O等高,圆弧轨道半径R=1.0m,现有一个质量为m=0.2kg可视为质点的小物体,从D点的正上方E点处自由下落,DE距离h=1.6m,物体与斜面AB之间的动摩擦因数μ=0.5.取sin37°=0.6,cos37°=0.8,g=10m/s2.求: