题目内容
8.如图(a)所示,两个完全相同的“人”字型金属轨道面对面正对着固定在竖直平面内,间距为d,它们的上端公共轨道部分保持竖直,下端均通过一小段弯曲轨道与一段直轨道相连,底端置于绝缘水平桌面上.MM′、PP′(图中虚线)之下的直轨道MN、M′N′、PQ、P′Q′长度均为L且不光滑(轨道其余部分光滑),并与水平方向均构成37°斜面,在左边轨道MM′以下的区域有垂直于斜面向下、磁感强度为B0的匀强磁场,在右边轨道PP′以下的区域有平行于斜面但大小未知的匀强磁场Bx,其它区域无磁场.QQ′间连接有阻值为2R的定值电阻与电压传感器(e、f为传感器的两条接线).另有长度均为d的两根金属棒甲和乙,它们与MM′、PP′之下的轨道间的动摩擦因数均为μ=$\frac{1}{8}$.甲的质量为m、电阻为R;乙的质量为2m、电阻为2R.金属轨道电阻不计.先后进行以下两种操作:
操作Ⅰ:将金属棒甲紧靠竖直轨道的左侧,从某处由静止释放,运动到底端NN′过程中棒始终保持水平,且与轨道保持良好电接触,计算机屏幕上显示的电压-时间关系图象U-t图如图(b)所示(图中U已知);
操作Ⅱ:将金属棒甲紧靠竖直轨道的左侧、金属棒乙(图中未画出)紧靠竖直轨道的右侧,在同一高度将两棒同时由静止释放.多次改变高度重新由静止释放,运动中两棒始终保持水平,发现两棒总是同时到达桌面.(sin37°=0.6,cos37°=0.8)

(1)试求操作Ⅰ中甲到MM′的速度大小;
(2)试求操作Ⅰ全过程定值电阻上产生的热量Q;
(3)试求右边轨道PP′以下的区域匀强磁场Bx的方向和大小.
分析 (1)根据图象求得电压对应的速度;
(2)由动能定理求得产生的热量;
(3)通过牛顿第二定律分别求得,两棒的加速度表达式,根据两者之间的关系确定力的关系.
解答  解:(1)由动能定理得:mgh=$\frac{1}{2}$mv12
解:(1)由动能定理得:mgh=$\frac{1}{2}$mv12
由图象知:棒进入磁场时定值电阻2R的电压为U,通过的电流为:
I1=$\frac{{B}_{0}d{v}_{1}}{3R}$
则有:U=I1×2R=$\frac{2{B}_{0}d{v}_{1}}{3}$
解得:v1=$\frac{3U}{2{B}_{0}d}$
(2)当甲棒离开磁场时的速度为v2,则有:2U=$\frac{2R}{3R}$B0dv2=$\frac{2}{3}$B0dv2
对甲棒,由动能定理,有:mgLsin37°-μmgLcos37°-Q总=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12
式中Q总为克服安培力所做的功,转化成了甲、乙棒上产生的热量;
故有:Q总=$\frac{1}{2}$mgL-$\frac{27m{U}^{2}}{8{B}_{0}^{2}{d}^{2}}$
定值电阻上产生的热量为:Q=$\frac{2}{3}$Q总=$\frac{1}{3}$mgL-$\frac{9m{U}^{2}}{4{B}_{0}^{2}{d}^{2}}$.
(3)由右手定则得:Bx沿斜面向下;
(两棒由静止释放的高度越高,甲棒进入磁场时的安培力越大,加速度越小,而乙棒只有摩擦力越大加速度才越小,故乙棒所受安培力应垂直斜面向下)
从不同高度下落两棒总是同时到达桌面,说明两棒运动的加速度时刻相同.
对甲棒,根据牛顿第二定律,有:mgsinθ-μmgcosθ-$\frac{{B}_{0}^{2}{d}^{2}v}{2R}$=ma
对乙棒,根据牛顿第二定律,有:2mgsinθ-μ(2mgcosθ+Bx×$\frac{1}{2}$×$\frac{{B}_{0}dv}{2R}$d)=2ma
则有:$\frac{μ{B}_{x}{B}_{0}{d}^{2}v}{8R}$=$\frac{{B}_{0}^{2}{d}^{2}v}{2R}$
解得:Bx=$\frac{4}{μ}$B0=32B0;
答:(1)则操作Ⅰ中甲到MM′的速度大小$\frac{3U}{2{B}_{0}d}$;
(2)则操作Ⅰ全过程定值电阻上产生的热量$\frac{1}{3}$mgL-$\frac{9m{U}^{2}}{4{B}_{0}^{2}{d}^{2}}$;
(3)则右边轨道PP′以下的区域匀强磁场Bx的方向沿斜面向和大小32B0
点评 本题要能正确读取图象的信息,准确分析能量的转化情况,由切割产生的感应电动势公式、闭合电路欧姆定律、共点力平衡、能量守恒等知识解答,综合性较强,需加强训练,提高解题能力.

 习题精选系列答案
习题精选系列答案 如图所示,竖直平面内有水平向左的匀强电场E,M点与P点的连线垂直电场线,M点与N点在同一条电场线上,两个完全相同的带等量正电荷的粒子,以相同的初速度大小v0分别从M点和N点沿竖直平面进入电场,重力不计,M点的粒子与电场线成一定的夹角进入,N点的粒子垂直电场线进入,两粒子恰好都能经过P点,在此过程中,下列说法正确的是( )
如图所示,竖直平面内有水平向左的匀强电场E,M点与P点的连线垂直电场线,M点与N点在同一条电场线上,两个完全相同的带等量正电荷的粒子,以相同的初速度大小v0分别从M点和N点沿竖直平面进入电场,重力不计,M点的粒子与电场线成一定的夹角进入,N点的粒子垂直电场线进入,两粒子恰好都能经过P点,在此过程中,下列说法正确的是( )| A. | 电场力对两粒子做功不相同 | |
| B. | 两粒子达到P点的速度大小可能相等 | |
| C. | 两粒子到达P点时的电势能都减少 | |
| D. | 两粒子到达P点所需时间一定不相等 |
 如图所示,两个质量分别为m1=1kg,m2=2kg的物体置于光滑水平面上,中间用轻质弹簧秤连接,两个大小分别为F1=4N、F2=10N的水平拉力分别作用在m1、m2上,则( )
如图所示,两个质量分别为m1=1kg,m2=2kg的物体置于光滑水平面上,中间用轻质弹簧秤连接,两个大小分别为F1=4N、F2=10N的水平拉力分别作用在m1、m2上,则( )| A. | 弹簧秤的示数是10N | |
| B. | 弹簧秤的示数是14N | |
| C. | 在突然撤去F1的瞬间,m2的加速度不变 | |
| D. | 在突然撤去F1的瞬间,m1的加速度大小为6m/s2 |
| A. | 非晶体呈各项同性,晶体呈各向异性 | |
| B. | 温度越高布朗运动越剧烈,颗粒越小布朗运动剧烈 | |
| C. | 当两个分子由无穷远逐渐靠近的时候,分子势能先增加后减小 | |
| D. | 热量能由高温物体传给低温物体,但是不能自发地低温物体传给高温物体 | |
| E. | 容器内一定质量的理想气体体积不变,温度升高,则单位时间内撞击容器壁的分子数增加 |
 如图所示,A为长木板,在水平面上以速度v1匀速向右运动,同时物块B在A的上表面以速度v2匀速向右运动,且A,B接触粗糙,下列判断正确的是( )
如图所示,A为长木板,在水平面上以速度v1匀速向右运动,同时物块B在A的上表面以速度v2匀速向右运动,且A,B接触粗糙,下列判断正确的是( )| A. | 若v1=v2,A、B之间无摩擦力 | |
| B. | 若v1>v2,A受到B所施加的滑动摩擦力向左 | |
| C. | 若v1<v2,B受到A所施加的滑动摩擦力向右 | |
| D. | 若v1>v2,A、B之间无滑动摩擦力 |
| A. | 出租汽车按位移的大小收费 | B. | 火车站售票厅悬挂的是列车时刻表 | ||
| C. | 只有运动物体才受滑动摩擦力 | D. | 力的大小可以用天平测量 |
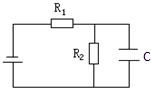 如图所示电路,电源的电动势为15V,内阻2Ω.R1=8Ω,R2=10Ω.平行板电容的电容为2μF,板间距离d=1cm.求电容器带的电量及板间电场强度.
如图所示电路,电源的电动势为15V,内阻2Ω.R1=8Ω,R2=10Ω.平行板电容的电容为2μF,板间距离d=1cm.求电容器带的电量及板间电场强度. 为“探究求合力的方法”的实验装置.
为“探究求合力的方法”的实验装置.