题目内容
3.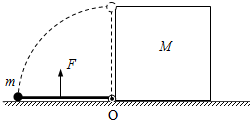 如图所示,长为L的轻杆一端连着质量为m的小球,另一端用活动铰链固接于水平地面上的O点,初始时小球静止于地面上,边长为L、质量为M的正方体左侧静止于O点处.现在杆中点处施加一大小始终为$\frac{6mg}{π}$(g为重力加速度)、方向始终垂直杆的拉力,经过一段时间后撤去F,小球恰好能到达最高点.忽略一切摩擦,试求:
如图所示,长为L的轻杆一端连着质量为m的小球,另一端用活动铰链固接于水平地面上的O点,初始时小球静止于地面上,边长为L、质量为M的正方体左侧静止于O点处.现在杆中点处施加一大小始终为$\frac{6mg}{π}$(g为重力加速度)、方向始终垂直杆的拉力,经过一段时间后撤去F,小球恰好能到达最高点.忽略一切摩擦,试求:(1)拉力所做的功;
(2)拉力撤去时小球的速度大小;
(3)若小球运动到最高点后由静止开始向右倾斜,求杆与水平面夹角为θ时(正方体和小球还未脱落),正方体的速度大小.
分析 (1)根据动能定理,抓住动能的变化量为零,求出力F做功的大小;
(2)根据F做功的大小求出杆与水平面夹角为α,根据动能定理得出撤去F时小球的速度;
(3)通过杆和正方体速度的关系,对系统运用机械能守恒求出正方体的速度大小.
解答 解:(1)根据动能定理可得:WF-mgL=0
力F所做的功为WF=mgL
(2)设撤去F时,杆与水平面夹角为α,撤去F前,有:
WF=$\frac{6mg}{π}$×$\frac{L}{2}$α=mgL,
解得:α=$\frac{π}{3}$
根据动能定理有:mgL-mgLsinα=$\frac{1}{2}$mv2
得撤去F时小球的速度为:v=$\sqrt{gL(2-\sqrt{3})}$
(3)设杆与水平面夹角为θ时,杆的速度为v1,正方体的速度为v2
v2=v1sinθ
系统机械能守恒有:
mg(L-Lsinθ)=$\frac{1}{2}$mv12+$\frac{1}{2}$Mv22
解得:v2=$\sqrt{\frac{2mgL(1-sinθ)si{n}^{2}θ}{m+Msi{n}^{2}θ}}$.
答:(1)力F所做的功为mgL;
(2)力F撤去时小球的速度为$\sqrt{gL(2-\sqrt{3})}$;
(3)正方体的速度大小为$\sqrt{\frac{2mgL(1-sinθ)si{n}^{2}θ}{m+Msi{n}^{2}θ}}$.
点评 本题考查了动能定理、机械能守恒的综合运用,对于第二问,抓住F做功的大小,求出杆与水平面夹角是解题的关键.以及知道杆和正方体组成的系统机械能守恒.

| A. | $\sqrt{2}$ | B. | $\root{3}{2}$ | C. | 2 | D. | $\root{3}{4}$ |
| A. | 哥白尼 | B. | 第谷 | C. | 伽利略 | D. | 开普勒 |
电流表(0~0.6A~3.0A)
电压表(0~3V~15V)
滑动变阻器R1(10Ω,2A)
滑动变阻器R2(100Ω,2A)
定值电阻R0(1.5Ω,2A)
电键S及导线若干.
(1)为方便实验调节且能较准确地进行测量,滑动变阻器应选用R1(填“R1”或“R2”).
(2)按照如图甲所示的电路连接线路,测得数据如表所示:
| 次数 待测量 | 1 | 2 | 3 | 4 | 5 |
| I/A | 0.15 | 0.20 | 0.30 | 0.40 | 0.50 |
| U/V | 1.46 | 1.45 | 1.43 | 1.42 | 1.39 |
(3)为使电压表的示数变化更明显,请将上述器材的连线略加改动,在图(乙)中画出改动后的实物连接图.

(4)实验中改变滑动变阻器的阻值,根据所测数据绘出U-I图线如图(丙)所示,则此干电池的内阻r=0.20Ω.(保留两位小数)
| A. | 人对物体做功21J | B. | 合外力对物体做功1J | ||
| C. | 物体的重力势能增加20J | D. | 物体的机械能增加20J |
 如图,一个小球从楼梯顶部以v0=2m/s的水平速度抛出,所有台阶都是高0.2m、宽0.25m.小球首先落到哪一台阶上( )
如图,一个小球从楼梯顶部以v0=2m/s的水平速度抛出,所有台阶都是高0.2m、宽0.25m.小球首先落到哪一台阶上( )| A. | 第二级 | B. | 第三级 | C. | 第四级 | D. | 第五级 |
| A. | 变压器可以改变直流电压 | |
| B. | 变压器是根据电磁感应原理工作的 | |
| C. | 变压器可以把其它形式的能转化为电能 | |
| D. | 变压器只能降低电压 |
 如图所示,在匀速转动的水平转盘上,有一个相对于转盘静止的物体M,下列关于它的受力情况分析正确的是( )
如图所示,在匀速转动的水平转盘上,有一个相对于转盘静止的物体M,下列关于它的受力情况分析正确的是( )| A. | 受重力和支持力的作用 | |
| B. | 受重力、支持力、向心力的作用 | |
| C. | 受重力、支持力、静摩擦的作用 | |
| D. | 受重力、支持力、静摩擦力,向心力的作用 |
 一群氢原子受激发后处于n=3能级,当它们向低能级跃迁 时,辐射的光照射光电管阴极K,发生光电效应,测得遏止电压Uc=10.8V.氢原子能级图如图所示,则逸出光电子的最大初动能为10.8eV;阴极K的逸出功为1.29 eV.
一群氢原子受激发后处于n=3能级,当它们向低能级跃迁 时,辐射的光照射光电管阴极K,发生光电效应,测得遏止电压Uc=10.8V.氢原子能级图如图所示,则逸出光电子的最大初动能为10.8eV;阴极K的逸出功为1.29 eV.