题目内容
10. 如图所示,小球由倾角为45°的斜坡底端P点正上方某一位置Q处自由下落,下落至P点的时间为t1,若小球从同一点Q处以速度v0水平向左抛出,恰好垂直撞在斜坡上,运动时间为t2,不计空气阻力,则t1:t2等于( )
如图所示,小球由倾角为45°的斜坡底端P点正上方某一位置Q处自由下落,下落至P点的时间为t1,若小球从同一点Q处以速度v0水平向左抛出,恰好垂直撞在斜坡上,运动时间为t2,不计空气阻力,则t1:t2等于( )| A. | 1:2 | B. | $\sqrt{3}$:1 | C. | 1:$\sqrt{2}$ | D. | 1:$\sqrt{3}$ |
分析 小球做平抛运动时,根据分位移公式求出竖直分速度和水平分速度之比,然后根据几何关系可求出自由落体运动的位移并求出时间.
解答 解:小球做平抛运动时,恰好能垂直落在斜坡上,有:
tan45°=$\frac{{v}_{0}}{{v}_{y}}$
又 vy=gt2,则得 t2=$\frac{{v}_{0}}{g}$
又 水平位移 s=v0t2
竖直位移 hQ=$\frac{1}{2}$gt22
由上得到:$\frac{{h}_{Q}}{s}$=$\frac{1}{2}$
小球做自由落体运动时,由几何关系可知小球下落的高度为:
hQ+s=$\frac{1}{2}$gt12
联立以上各式解得:$\frac{{t}_{1}}{{t}_{2}}$=$\frac{\sqrt{3}}{1}$.故B正确,A、C、D错误.
故选:B
点评 本题关键是明确小球Q的运动是平抛运动,然后根据平抛运动的分位移和分速度公式联立求解出运动时间,再根据几何关系得到自由落体的位移,从而进一步求得时间,最后得到比值.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
20.下列说法正确的是( )
| A. | 光纤通信,全息照相及医用纤维是内窥镜都是利用了光的全反射原理 | |
| B. | 做双缝干涉实验时,用绿光照射单缝,在光屏P上观察到干涉条纹,用红光代替绿光照射单缝将得到相邻条纹间距更大的干涉图样 | |
| C. | 相对论认为:竖直向上高速运动的球在水平方向上变扁了 | |
| D. | 在真空中传播的电磁波,当它的频率增加时,它的传播速度不变,波长变短 |
1.某人站在静止于光滑水平面上的平板车上,若人从车头走向车尾,人和车的运动情况为( )
| A. | 人匀速走动,则车匀速前进,人和车对地位移大小与其质量成反比 | |
| B. | 人匀加速走动,车匀加速前进,两者对地加速度相等 | |
| C. | 不管人如何走,任意时刻人和车动量总相同 | |
| D. | 人停止走动时,车的速度不一定为0 |
18.一质点做匀加速直线运动,并规定了正方向.若已知质点在一段时间t内的末速度v及加速度a,则质点此段运动的位移可表示为( )
| A. | $vt+\frac{1}{2}a{t^2}$ | B. | $-vt+\frac{1}{2}a{t^2}$ | C. | $-vt-\frac{1}{2}a{t^2}$ | D. | $vt-\frac{1}{2}a{t^2}$ |
15.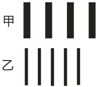 a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )
a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )
 a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )
a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )| A. | a光的频率比b光大 | B. | b光比a光易发生衍射现象 | ||
| C. | a光比b光易发生全反射现象 | D. | b光在水中的传播速度较小 |
2.某实验小组利用如下实验器材测量干电池的电动势和内阻.
A.待测干电池两节,每节电池电动势约为1.5V,内阻约几欧姆
B.直流电压表V1、V2,内阻约为3kΩ
C.阻值为5Ω的定值电阻R0
D.滑动变阻器R,最大阻值Rm
E.导线和开关
(1)根据下面图1电路原理图完成图2电路实物图的连接;

(2)实验中移动滑动变阻器触头,读出电压表V1和V2的多组数据如下表,请在图3的坐标纸中描绘出U1-U2图象;
(2)根据描绘出的U1-U2图象,求得两节干电池的总电动势E=3.0V,总内阻r=2.5Ω(计算结果保留两位有效数字).
A.待测干电池两节,每节电池电动势约为1.5V,内阻约几欧姆
B.直流电压表V1、V2,内阻约为3kΩ
C.阻值为5Ω的定值电阻R0
D.滑动变阻器R,最大阻值Rm
E.导线和开关
(1)根据下面图1电路原理图完成图2电路实物图的连接;

(2)实验中移动滑动变阻器触头,读出电压表V1和V2的多组数据如下表,请在图3的坐标纸中描绘出U1-U2图象;
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| U1(V) | 0.50 | 0.81 | 1.00 | 1.50 | 1.85 | 2.30 |
| U2(V) | 2.15 | 2.21 | 2.32 | 2.50 | 2.69 | 2.76 |
19. 如图所示,杂技演员在一根两端周定的水平弹性绳上表演,演员从某一高度下落,落到绳上的A后向下运动,使弹性绳发生形变,B是演员运动到的最低点,不计弹性绳的质量和空气阻力不计,则( )
如图所示,杂技演员在一根两端周定的水平弹性绳上表演,演员从某一高度下落,落到绳上的A后向下运动,使弹性绳发生形变,B是演员运动到的最低点,不计弹性绳的质量和空气阻力不计,则( )
 如图所示,杂技演员在一根两端周定的水平弹性绳上表演,演员从某一高度下落,落到绳上的A后向下运动,使弹性绳发生形变,B是演员运动到的最低点,不计弹性绳的质量和空气阻力不计,则( )
如图所示,杂技演员在一根两端周定的水平弹性绳上表演,演员从某一高度下落,落到绳上的A后向下运动,使弹性绳发生形变,B是演员运动到的最低点,不计弹性绳的质量和空气阻力不计,则( )| A. | 从A到B的运动过程中,演员的机械能保持不变 | |
| B. | 从A到B的运动过程中,演员的动能不断减少 | |
| C. | 从A到B的运动过程中,演员重力做的功等于其重力势能的减小量 | |
| D. | 从A到B的运动过程中,演员重力做的功大于克服绳支持力做的功 |
 如图,一长为L、质量为m的光滑均匀细长杆,可绕固定在水平地面的铰链自由转动.一边长为a的正方体置于光滑水平地面上.开始时杆搁在正方体上,并用一水平外力顶住正方体,使系统处于静止状态,此时杆与水平面间夹角为60°,则外力的大小为$\frac{\sqrt{3}mgL}{16a}$.现撤去外力,当杆与水平面间夹角变为α时(杆与正方体尚未分离)杆的转动角速度大小为ω,则此时正方体移动的速度大小为$\frac{ωa}{si{n}^{2}α}$.(重力加速度为g)
如图,一长为L、质量为m的光滑均匀细长杆,可绕固定在水平地面的铰链自由转动.一边长为a的正方体置于光滑水平地面上.开始时杆搁在正方体上,并用一水平外力顶住正方体,使系统处于静止状态,此时杆与水平面间夹角为60°,则外力的大小为$\frac{\sqrt{3}mgL}{16a}$.现撤去外力,当杆与水平面间夹角变为α时(杆与正方体尚未分离)杆的转动角速度大小为ω,则此时正方体移动的速度大小为$\frac{ωa}{si{n}^{2}α}$.(重力加速度为g)