一化工厂因排污趋向严重,2011年1月决定着手整治.经调研,该厂第一个月的污染度为60,整治后前四个月的污染度如下表;
| 月数 | 1 | 2 | 3 | 4 | … |
| 污染度 | 60 | 31 | 13 | 0 | … |
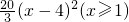 ,h(x)=30|log2x-2|(x≥1),其中x表示月数,f(x),g(x),h(x)分别表示污染度.(参考数据:lg2=0.3010,lg3=0.4771)
,h(x)=30|log2x-2|(x≥1),其中x表示月数,f(x),g(x),h(x)分别表示污染度.(参考数据:lg2=0.3010,lg3=0.4771)(Ⅰ)问选用哪个函数模拟比较合理,并说明理由;
(Ⅱ)如果环保部门要求该厂每月的排污度均不能超过60,若以比较合理的模拟函数预测,该厂最晚在何时开始进行再次整治?
 (e是自然对数的底数),g(x)=ax(a是实数).
(e是自然对数的底数),g(x)=ax(a是实数). 的图象关于点P对称,则点P的坐标是
的图象关于点P对称,则点P的坐标是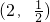


 ,b=20.3,c=0.30.2,则a,b,c三者的大小关系是________.
,b=20.3,c=0.30.2,则a,b,c三者的大小关系是________.