题目内容
锐角△ABC中,A,B,C成等差数列,边b=1,则边a的取值范围________.
( ,
, )
)
分析:根据A、B、C成等差数列结合内角和定理,可得B= .由b=1结合正弦定理算出a=
.由b=1结合正弦定理算出a= sinA,再根据△ABC是锐角三角形算出A∈(
sinA,再根据△ABC是锐角三角形算出A∈( ,
, ),结合正弦函数的性质即可得到边a的取值范围.
),结合正弦函数的性质即可得到边a的取值范围.
解答:∵A+B+C=π,且A、B、C成等差数列,∴B=
又∵b=1,可得 =
=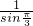 =
=
∴由正弦定理,得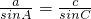 =
= ,可得a=
,可得a= sinA
sinA
∵锐角△ABC中,B= ,
,
∴结合A+C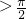 ,可得A∈(
,可得A∈( ,
, )
)
∴sinA∈(sin ,sin
,sin ),即sinA∈(
),即sinA∈( ,1),
,1),
因此,a= sinA∈(
sinA∈( ,
, )
)
故答案为:( ,
, )
)
点评:本题给出锐角三角形ABC的内角成等差数列,在已知b=1的情况下求边a的取值范围,着重考查了用正余弦定理解三角形、等差数列和三角函数的图象与性质等知识,属于基础题.
 ,
, )
)分析:根据A、B、C成等差数列结合内角和定理,可得B=
 .由b=1结合正弦定理算出a=
.由b=1结合正弦定理算出a= sinA,再根据△ABC是锐角三角形算出A∈(
sinA,再根据△ABC是锐角三角形算出A∈( ,
, ),结合正弦函数的性质即可得到边a的取值范围.
),结合正弦函数的性质即可得到边a的取值范围.解答:∵A+B+C=π,且A、B、C成等差数列,∴B=

又∵b=1,可得
 =
=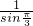 =
=
∴由正弦定理,得
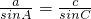 =
= ,可得a=
,可得a= sinA
sinA∵锐角△ABC中,B=
 ,
,∴结合A+C
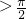 ,可得A∈(
,可得A∈( ,
, )
)∴sinA∈(sin
 ,sin
,sin ),即sinA∈(
),即sinA∈( ,1),
,1),因此,a=
 sinA∈(
sinA∈( ,
, )
)故答案为:(
 ,
, )
)点评:本题给出锐角三角形ABC的内角成等差数列,在已知b=1的情况下求边a的取值范围,着重考查了用正余弦定理解三角形、等差数列和三角函数的图象与性质等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目