某港口海水的深度y(米)是时间t(时)(0≤t≤24)的函数,记为:y=f(t).
已知某日海水深度的数据如下:
经长期观察,y=f(t)的曲线可近似地看成函数y=Asinωt+b的图象.
(1)试根据以上数据,求出函数y=f(t)=Asinωt+b的振幅、最小正周期和表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)?
0 77127 77135 77141 77145 77151 77153 77157 77163 77165 77171 77177 77181 77183 77187 77193 77195 77201 77205 77207 77211 77213 77217 77219 77221 77222 77223 77225 77226 77227 77229 77231 77235 77237 77241 77243 77247 77253 77255 77261 77265 77267 77271 77277 77283 77285 77291 77295 77297 77303 77307 77313 77321 266669
已知某日海水深度的数据如下:
| t(时) | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | |
| y(米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)试根据以上数据,求出函数y=f(t)=Asinωt+b的振幅、最小正周期和表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)?
 有下列命题:其中正确的是( )
有下列命题:其中正确的是( ) ;
; 对称;
对称; 对称;
对称; 上是增函数.
上是增函数.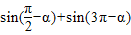 的值为 .
的值为 . 的定义域是 .
的定义域是 . 的图象上所有的点向右平行移动
的图象上所有的点向右平行移动 个单位长度,再把所得图象各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是 .
个单位长度,再把所得图象各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是 . =(m,n),
=(m,n), =(p,q),令
=(p,q),令 ?
? =mq-np,给出下面五个判断:
=mq-np,给出下面五个判断: 与
与 共线,则
共线,则 ?
? =0;
=0; 与
与 垂直,则
垂直,则 ?
? =0;
=0; ?
? =
= ?
? ;
; ;
; ?
? )2+2=|
)2+2=| |2|
|2| |2
|2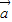 =(1,-2),
=(1,-2),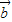 =(-3,2),
=(-3,2),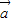 +
+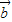 )•(
)•(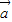 -2
-2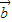 )的值.
)的值.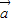 +
+ 与
与 -3
-3 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向? 且
且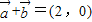 ,
,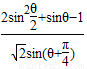 的值.
的值.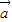 ,
,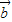 的夹角为60°,且|
的夹角为60°,且|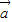 |=2,|
|=2,|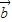 |=1,若
|=1,若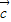 =
=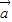 -4
-4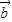 ,
,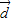 =
=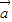 +2
+2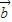 ,
,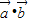 及|
及|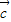 +
+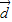 |值?
|值?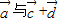 的夹角?
的夹角? ,
, ,且f(x)=
,且f(x)= ×
×
 时,f(x)的最小值是-4,求此时函数f(x)的最大值,并求出相应的x的值.
时,f(x)的最小值是-4,求此时函数f(x)的最大值,并求出相应的x的值.