题目内容
已知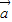 =(1,-2),
=(1,-2),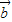 =(-3,2),
=(-3,2),(1)求(
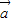 +
+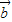 )•(
)•(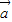 -2
-2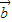 )的值.
)的值.(2)当k为何值时,k
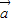 +
+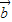 与
与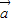 -3
-3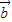 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
【答案】分析:(1)由已知两个向量的坐标,可得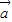 2,
2,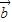 2,
2,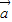 •
•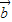 的值,利用乘法公式将(
的值,利用乘法公式将(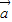 +
+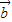 )(
)(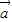 -2
-2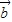 )展开,代入可得答案.
)展开,代入可得答案.
(2)分别求出k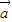 +
+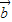 与
与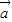 -3
-3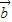 坐标,根据向量平行的充要条件,构造关于k的方程,解方程求出k值,进而根据数乘向量的几何意义,可判断两个向量的方向.
坐标,根据向量平行的充要条件,构造关于k的方程,解方程求出k值,进而根据数乘向量的几何意义,可判断两个向量的方向.
解答:解:(1)∵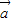 =(1,-2),
=(1,-2),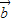 (-3,2),
(-3,2),
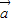 2=5,
2=5,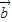 2=13,
2=13,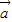 •
•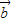 =-7,
=-7,
∴(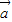 +
+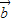 )•(
)•(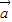 -2
-2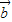 )=
)=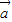 2-2
2-2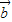 2-
2-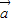 •
•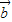 =-14,
=-14,
(2)∵k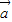 +
+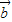 =(k-3,-2k+2),
=(k-3,-2k+2),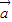 -3
-3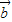 =(10,-8)
=(10,-8)
由k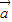 +
+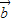 与
与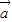 -3
-3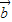 平行,
平行,
则有:-8×(k-3)-10×(-k+2)=0
得:k=- ,
,
则-
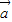 +
+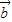 =-
=- (
(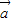 -3
-3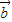 )
)
即两个向量是反向的.
点评:本题考查的知识点是平面向量数量积的运算,平行向量与共线向量,熟练掌握平面向量的运算法则及向量共线的充要条件是解答的关键.
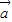 2,
2,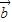 2,
2,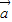 •
•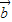 的值,利用乘法公式将(
的值,利用乘法公式将(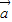 +
+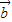 )(
)(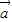 -2
-2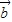 )展开,代入可得答案.
)展开,代入可得答案.(2)分别求出k
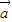 +
+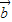 与
与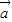 -3
-3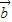 坐标,根据向量平行的充要条件,构造关于k的方程,解方程求出k值,进而根据数乘向量的几何意义,可判断两个向量的方向.
坐标,根据向量平行的充要条件,构造关于k的方程,解方程求出k值,进而根据数乘向量的几何意义,可判断两个向量的方向.解答:解:(1)∵
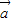 =(1,-2),
=(1,-2),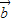 (-3,2),
(-3,2),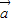 2=5,
2=5,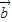 2=13,
2=13,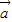 •
•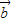 =-7,
=-7,∴(
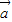 +
+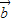 )•(
)•(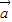 -2
-2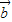 )=
)=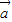 2-2
2-2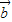 2-
2-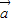 •
•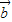 =-14,
=-14,(2)∵k
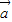 +
+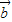 =(k-3,-2k+2),
=(k-3,-2k+2),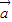 -3
-3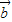 =(10,-8)
=(10,-8)由k
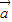 +
+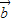 与
与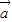 -3
-3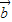 平行,
平行,则有:-8×(k-3)-10×(-k+2)=0
得:k=-
 ,
,则-

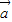 +
+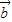 =-
=- (
(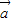 -3
-3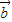 )
)即两个向量是反向的.
点评:本题考查的知识点是平面向量数量积的运算,平行向量与共线向量,熟练掌握平面向量的运算法则及向量共线的充要条件是解答的关键.

练习册系列答案
相关题目