(本题9分)给出下面的数表序列:
| 表1 | 表2 | 表3 | … |
| 1 | 1 3 | 1 3 5 | |
| | 4 | 4 8 | |
| | | 12 | |
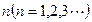 有
有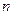 行,第1行的
行,第1行的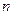 个数
个数 是1,3,5,…,
是1,3,5,…, ,从第2行起,每行中的每个数都等于它肩上的两数之和。
,从第2行起,每行中的每个数都等于它肩上的两数之和。(1)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表
 (不要求证明)
(不要求证明)(2)每个数表中最后一行都只有一个数,它们构成数列1,4,12,…,记此数列为
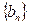 ,求数列
,求数列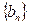 的前
的前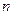 项和
项和 (本题9分)给出下面的数表序列:
| 表1 | 表2 | 表3 | … |
| 1 | 1 3 | 1 3 5 | |
| | 4 | 4 8 | |
| | | 12 | |
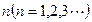 有
有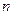 行,第1行的
行,第1行的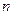 个数
个数 是1,3,5,…,
是1,3,5,…, ,从第2行起,每行中的每个数都等于它肩上的两数之和。
,从第2行起,每行中的每个数都等于它肩上的两数之和。 (不要求证明)
(不要求证明)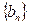 ,求数列
,求数列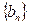 的前
的前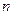 项和
项和