设f(x)=asin(πx+α)+bcos(πx+β)+4,其中a、b、α、β均为非零实数,若f(1988)=3,则f(2013)的值为( )
|
| A. | 1 | B. | 5 | C. | 3 | D. | 不确定 |
已知函数f(x)=2sin(ωx+φ)对任意x都有![]() ,则
,则![]() 等于( )
等于( )
|
| A. | 2或0 | B. | ﹣2或2 | C. | 0 | D. | ﹣2或0 |
设y=f(x)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24,下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象,下面的函数中,最能近似表示表中数据间对应关系的函数是(t∈[0,24])( )
|
| A. |
| B. |
|
|
| C. |
| D. |
|
为了得到函数y=sin(2x﹣![]() )的图象,可以将函数y=cos2x的图象( )
)的图象,可以将函数y=cos2x的图象( )
|
| A. | 向右平移 | B. | 向右平移 |
|
| C. | 向左平移 | D. | 向左平移 |
函数y=2sin(![]() ﹣2x)(x∈[0,π])为增函数的区间是( )
﹣2x)(x∈[0,π])为增函数的区间是( )
|
| A. | [0, | B. | [ | C. | [ | D. | [ |
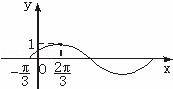
若函数f(x)=sin(ωx+φ)的图象(部分)如下图所示,则ω和φ的取值是( )
|
| A. | ω=1,φ= | B. | ω=1,φ=﹣ | C. | ω= | D. | ω= |
在函数y=|tanx|,y=|sin(x+![]() )|,y=|sin2x|,y=sin(2x﹣
)|,y=|sin2x|,y=sin(2x﹣![]() )四个函数中,既是以π为周期的偶函数,又是区间(0,
)四个函数中,既是以π为周期的偶函数,又是区间(0,![]() )上的增函数个数是( )
)上的增函数个数是( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
下列四个命题正确的是( )
|
| A. | sin2<sin3<sin4 | B. | sin4<sin2<sin3 | C. | sin3<sin4<sin2 | D. | sin4<sin3<sin2 |
已知点P(tanα,cosα)在第三象限,则角α的终边在第几象限( )
|
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
cos510°的值为( )
|
| A. |
| B. |
| C. | ﹣ | D. | ﹣ |