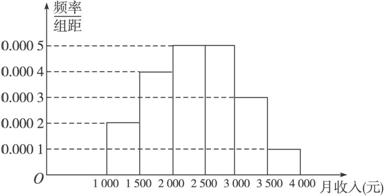
下表是我国居民生活污水排放量的一组数据:
年份 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
排放量 | 151 |
| 189.1 | 194.8 | 203.8 | 220.9 | 227.7 | 232.3 |
试估计1998年我国居民生活污水排放量,并预测2006年生活污水排放量.(单位:102t)
随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司为此一次抽样调查,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如下的数据资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若有资料知,y对x呈线性相关关系.试求:
(1)线性回归方程![]() =bx+a的回归系数a、b;
=bx+a的回归系数a、b;
(2)估计使用年限为10年时,车的使用总费用是多少?
某医院用光电比色计检验尿汞时,得尿汞含量(mg/L)与消光系数如下表:
尿汞含量x | 2 | 4 | 6 | 8 | 10 |
消光系数y | 64 | 138 | 205 | 285 | 360 |
(1)用统计方法判断尿汞含量x与消光系数y是否相关?
(2)求出回归直线方程.
(3)能预测尿汞含量为5 mg/L时的消光系数吗?
高二·二班学生每周用于数学学习的时间x(单位:h)与数学成绩y(单位:分)之间有如下数据:
x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
某同学每周用于数学学习的时间为18 h,试预测该生数学成绩.
设对变量x、y有如下观察的数据:
x | 151 | 152 | 153 | 154 | 156 | 157 | 158 | 160 | 160 | 162 | 163 | 164 |
y | 40 | 41 | 41 | 41.5 | 42 | 42.5 | 43 | 44 | 45 | 45 | 46 | 45.5 |
(1)画出散点图;
(2)如果变量x、y有线性关系,求出回归直线方程.
下表是某地的年降雨量与年平均气温,判断两者是相关关系吗?求回归直线方程有意义吗?
0 52983 52991 52997 53001 53007 53009 53013 53019 53021 53027 53033 53037 53039 53043 53049 53051 53057 53061 53063 53067 53069 53073 53075 53077 53078 53079 53081 53082 53083 53085 53087 53091 53093 53097 53099 53103 53109 53111 53117 53121 53123 53127 53133 53139 53141 53147 53151 53153 53159 53163 53169 53177 266669
年平均气温(℃) | 12.51 | 12.84 | 12.84 | 13.69 | 13.33 | 12.47 | 13.05 |
年降雨量(mm) | 748 | 542 | 507 | 813 | 574 | 701 | 432 |