编号为A1,A2,…,A16的16名篮球运动员在某次训练比赛中的得分记录如下:
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
(Ⅱ)从得分在区间[20,30)内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50分的概率.
| 运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
| 得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
| 运动员编号 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| 得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
| 区间 | [10,20) | [20,30) | [30,40] |
| 人数 |
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50分的概率.
对实数a与b,定义新运算“?”:a?b=
.设函数f(x)=(x2-2)?(x-1),x∈R.若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
|
| A、(-1,1]∪(2,+∞) |
| B、(-2,-1]∪(1,2] |
| C、(-∞,-2)∪(1,2] |
| D、[-2,-1] |
已知函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,-π<φ≤π.若函数f(x)的最小正周期为6π,且当x=
时,f(x)取得最大值,则( )
| π |
| 2 |
| A、f(x)在区间[-2π,0]上是增函数 |
| B、f(x)在区间[-3π,-π]上是增函数 |
| C、f(x)在区间[3π,5π]上是减函数 |
| D、f(x)在区间[4π,6π]上是减函数 |
已知双曲线
-
=1(a>0,b>0)的左顶点与抛物线y2=2px的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、2
| ||
B、2
| ||
C、4
| ||
D、4
|
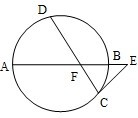 如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且 DF=CF=
如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且 DF=CF= 10、一个几何体的三视图如图所示(单位:m),则这个几何体的体积为
10、一个几何体的三视图如图所示(单位:m),则这个几何体的体积为