一个均匀的正四面体的四个面上分别涂有1，2，3，4四个数字，现随机投掷两次，正四面体面朝下的数字分别为x1，x2，记ξ=（x1-3）2+（x2-3）2．
（1）分别求出ξ取得最大值和最小值时的概率；
（2）求ξ的分布列及数学期望．
0
在棱长为2的正方体AC1中，G是AA1的中点，则BD到平面GB1D1的距离是（　　）
A、
6
3
B、
2
6
3
C、
2
3
3
D、
2
3
1、定义A-B={x|x∈A且x∉B}，若M={x∈N|y=lg（6x-x2）}，N={2，3，6}，是N-M等于（　　）
已知α、β为锐角，
a
=（cosα，sinα），
b
=（cosβ，sinβ），
c
=（
1
2
，-
1
2
），
a
•
b
=
2
2
，
a
•
c
=
3
-1
4
，求角2β-α的值．
设α是第二象限的角，tanα=-
4
3
，且sin
α
2
＜cos
α
2
，则cos
α
2
=
 
．
已知tanα和tan（
π
4
-α）是方程ax2+bx+c=0的两个根，则a、b、c的关系是（　　）
A、b=a+c
B、2b=a+c
C、c=b+a
D、c=ab
定义运算
.
ab
cd
.
=ad-bc、若cosα=
1
7
，
.
sinαsinβ
cosαcosβ
.
=
3
3
14
，0＜β＜α＜
π
2
，则β等于（　　）
A、
π
12
B、
π
6
C、
π
4
D、
π
3
sin(180°+2α)
1+cos2α
•
cos2α
cos(90°+α)
等于（　　）
A、-sinαB、-cosα
C、sinαD、cosα
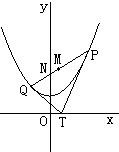精英家教网过x轴上的动点T（t，0），引抛物线y=x2+1两条切线TP，TQ，P，Q为切点．
（Ⅰ）求证：直线PQ过定点N，并求出定点N坐标；
（Ⅱ）若t≠0，设弦PQ的中点为M，试求S△OTM|OT|的最小值（O为坐标原点）．
 0  31279  31287  31293  31297  31303  31305  31309  31315  31317  31323  31329  31333  31335  31339  31345  31347  31353  31357  31359  31363  31365  31369  31371  31373  31374  31375  31377  31378  31379  31381  31383  31387  31389  31393  31395  31399  31405  31407  31413  31417  31419  31423  31429  31435  31437  31443  31447  31449  31455  31459  31465  31473  266669 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网