等差数列{an}中,公差d=-
,a7=8,前n项和为Sn,则S10=( )
| 1 |
| 3 |
| A、85 | B、105 |
| C、120 | D、125 |
已知复数z与(z-2)2-8i均为纯虚数,则z=( )
| A、.2i | B、-2i | C、±2i | D、i |
设f(x)=
,则
f(x)dx=( )
|
| ∫ | 2 -1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
| ∫ |
0 |
| x |
| 2 |
A、-
| ||||
| B、1 | ||||
C、
| ||||
D、
|
设函数f(x)在区间[a,b]上连续,用分点a=x0<x1<…<xi-1<xi…<xn=b,把区间[a,b]等分成n个小区间,在每个小区间[xi-1,xi]上任取一点ξi(i=1,2,…,n),作和式Sn=
f(ξi)△x(其中△x为小区间的长度),那么Sn的大小( )
| n |
 |
| i=1 |
| A、与f(x)和区间[a,b]有关,与分点的个数n和ξi的取法无关 |
| B、与f(x)和区间[a,b]和分点的个数n有关,与ξi的取法无关 |
| C、与f(x)和区间[a,b]和分点的个数n,ξi的取法都有关 |
| D、与f(x)和区间[a,b]和ξi取法有关,与分点的个数n无关 |
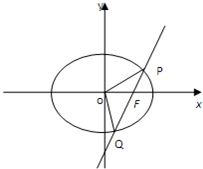 已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点.
已知直线l过椭圆E:x2+2y2=2的右焦点F,且与E相交于P,Q两点. 10、如图,如果输入三个实数a、b、c,要求输出这三个数中最小的数,那么在空白的判断框中,应该填入下面四个选项中的( )
10、如图,如果输入三个实数a、b、c,要求输出这三个数中最小的数,那么在空白的判断框中,应该填入下面四个选项中的( )