题目内容
设f(x)=
,则
f(x)dx=( )
|
| ∫ | 2 -1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:利用定积分的运算法则,找出被积函数的原函数,同时注意通过对被积函数中的x进行分类讨论,结合分段函数的解析化简后进行计算.
解答:解:
f(x)dx
=∫-11x2dx+∫12(2-x)dx
=(
x3)|-11+(2x-
x2)|12
=
.
故选D.
| ∫ | 2 -1 |
=∫-11x2dx+∫12(2-x)dx
=(
| 1 |
| 3 |
| 1 |
| 2 |
=
| 7 |
| 6 |
故选D.
点评:本题主要考查定积分的基本运算,解题关键是找出被积函数的原函数,利用分段函数也是注意点,本题属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
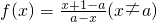
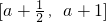 时,求f(x)的值域;
时,求f(x)的值域;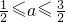 ,求g(x)的最小值.
,求g(x)的最小值.