已知函数地f(x)=3x+cos2x+sin2x且a=f′(π4).f′(x)是f(x)的导函数.则过曲线y=x3上一点P A.3x-y-2=0B.4x-3y+1=0C.3x-y-2——青夏教育精英家教网——

已知函数地f（x）=3x+cos2x+sin2x且a=f′(

)，f′(x)是f（x）的导函数，则过曲线y=x³上一点P（a，b）的切线方程为（　　）

C、3x-y-2=0或3x-4y+1=0

D、3x-y-2=0或4x-3y+1=0

设随机变量ξ-N（μ，1），若不等式x2-

≥0对任意实数x都成立，且P（ξ＞a）=

，则μ的值为（　　）

若将（x-a）（x-b）逐项展开得x²-ax-bx+ab，则x²出现的频率为

，x出现的频率为

，如此将（x-a）（x-b）（x-c）（x-d）（x-e）逐项展开后，x³出现的频率是（　　）

某服装加工厂某月生产A、B、C三种产品共4000件，为了保证产品质量，进行抽样检验，根据分层抽样的结果，企业统计员制作了如下的统计表格：

产品类别	A	B	C
产品数量（件）		2300
样本容量（件）		230

由于不小心，表格中A、C产品的有关数据已被污染看不清楚，统计员记得A产品的样本容量比C产品的样本容量多10，根据以上信息，可得C的产品数量是（　　）

A、80	B、800
C、90	D、900

2、数列a_n是等差数列，公差d不为0，且a₂₀₄₆+a₁₉₇₈-a²₂₀₁₂=0，b_n是等比数列，且b₂₀₁₂=a₂₀₁₂，则b₂₀₁₀•b₂₀₁₄=（　　）

已知双曲线 2x²-2y²=1的两个焦点为F₁，F₂，P为动点，若|PF₁|+|PF₂|=4．
（Ⅰ）求动点P的轨迹E的方程；
（Ⅱ）求cos∠F₁PF₂的最小值；
（Ⅲ）设点M（-2，0），过点N（-

，0）作直线l交轨迹E于A、B两点，判断∠AMB的大小是否为定值？并证明你的结论．

已知函数f(x)=

-ln(ax)+ln(x+1)，（a≠0，a∈R）
（Ⅰ）求函数f（x）的定义域；
（Ⅱ）求函数f（x）的单调区间；
（Ⅲ）当a＞0时，若存在x使得f（x）≥ln（2a）成立，求a的取值范围．

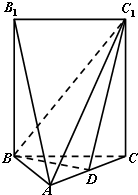如图，五面体A-BCC₁B₁中，AB₁=4．底面ABC 是正三角形，AB=2．四边形BCC₁B₁是矩形，二面角A-BC-C₁为直二面角．
（Ⅰ）D在AC上运动，当D在何处时，有AB₁∥平面BDC₁，并且说明理由；
（Ⅱ）当AB₁∥平面BDC₁时，求二面角C-BC₁-D余弦值．

函数f(x)=Asin(ωx+φ)+B(A＞0，ω＞0，|φ|＜

)的图象上一个最高点的坐标为 (

，3)，与之相邻的一个最低点的坐标为 (

，-1)．
（Ⅰ）求f（x）的表达式；
（Ⅱ）当x∈[

，π]，求函数f（x）的单调递增区间和零点．

抛掷3个骰子，当至少有一个5点或一个6点出现时，就说这次试验成功，则在54次试验中成功次数n的期望为

0 30460 30468 30474 30478 30484 30486 30490 30496 30498 30504 30510 30514 30516 30520 30526 30528 30534 30538 30540 30544 30546 30550 30552 30554 30555 30556 30558 30559 30560 30562 30564 30568 30570 30574 30576 30580 30586 30588 30594 30598 30600 30604 30610 30616 30618 30624 30628 30630 30636 30640 30646 30654 266669