在研究并行计算的基本算法时,有以下简单模型问题:
用计算机求n个不同的数v1,v2,…,vn的和
vi=v1+v2+v3+…+vn.计算开始前,n个数存贮在n台由网络连接的计算机中,每台机器存一个数,计算开始后,在一个单位时间内,每台机器至多到一台其他机器中读数据,并与自己原有数据相加得到新的数据,各台机器可同时完成上述工作.为了用尽可能少的单位时间,使各台机器都得到这n个数的和,需要设计一种读和加的方法.比如n=2时,一个单位时间即可完成计算,方法可用下表表示:
(Ⅰ)当n=4时,至少需要多少个单位时间可完成计算?把你设计的方法填入下表
(Ⅱ)当n=128时,要使所有机器都得到
vi,至少需要多少个单位时间可完成计算?(结论不要求证明)
用计算机求n个不同的数v1,v2,…,vn的和
| n |
 |
| i=1 |
| 机器号 | 初始时 | 第一单位时间 | 第二单位时间 | 第三单位时间 | |||
| 被读机号 | 结 果 | 被读机号 | 结 果 | 被读机号 | 结 果 | ||
| 1 | v1 | 2 | v1+v2 | ||||
| 2 | v2 | 1 | v2+v1 | ||||
| 机器号 | 初始时 | 第一单位时间 | 第二单位时间 | 第三单位时间 | |||
| 被读机号 | 结 果 | 被读机号 | 结 果 | 被读机号 | 结 果 | ||
| 1 | v1 | ||||||
| 2 | v2 | ||||||
| 3 | v3 | ||||||
| 4 | v4 | ||||||
| n |
 |
| i=1 |
如图所示,f1(x),f2(x),f3(x),f4(x)是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的x1和x2,f(
)≤
[f(x1)+f(x2)]恒成立”的只有( )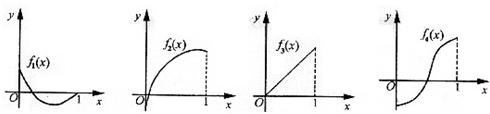
| x1+x2 |
| 2 |
| 1 |
| 2 |

| A、f1(x),f3(x) |
| B、f2(x) |
| C、f2(x),f3(x) |
| D、f4(x) |
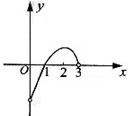 已知f(x)的定义在(0,3)上的函数,f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是( )
已知f(x)的定义在(0,3)上的函数,f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是( )| A、(0,1)∪(2,3) | ||||
B、(1,
| ||||
C、(0,1)∪(
| ||||
| D、(0,1)∪(1,3) |
已知椭圆
+
=1和双曲线
-
=1有公共的焦点,那么双曲线的渐近线方程是( )
| x2 |
| 3m2 |
| y2 |
| 5n2 |
| x2 |
| 2m2 |
| y2 |
| 3n2 |
A、x=±
| ||||
B、y=±
| ||||
C、x=±
| ||||
D、y=±
|
若
=1,则cos2θ的值为( )
| cotθ-1 |
| 2cotθ+1 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
(1+i)8等于( ).
| A、16i | B、-16i | C、-16 | D、16 |
64个直径都为
的球,记它们的体积之和为V甲,表面积之和为S甲;一个直径为a的球,记其体积为V乙,表面积为S乙,则( )
| a |
| 4 |
| A、V甲>V乙且S甲>S乙 |
| B、V甲<V乙且S甲<S乙 |
| C、V甲=V乙且S甲>S乙 |
| D、V甲=V乙且S甲=S乙 |
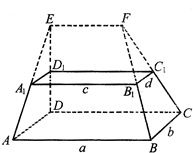 如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h.
如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h.