题目内容
如图所示,f1(x),f2(x),f3(x),f4(x)是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的x1和x2,f(
)≤
[f(x1)+f(x2)]恒成立”的只有( )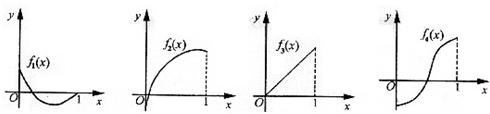
| x1+x2 |
| 2 |
| 1 |
| 2 |

| A、f1(x),f3(x) |
| B、f2(x) |
| C、f2(x),f3(x) |
| D、f4(x) |
分析:此题考查的是函数图象的应用问题.在解答时,应先充分结合条件:“对[0,1]中任意的x1和x2,f(
)≤
[f(x1)+f(x2)]恒成立”分析函数的凸凹性,进而根据具体的变化规律作出判断.
| x1+x2 |
| 2 |
| 1 |
| 2 |
解答:解:由题意可知:函数f(x)满足性质:“对[0,1]中任意的x1和x2,f(
)≤
[f(x1)+f(x2)]恒成立”.
∴函数图象在[0,1]上为下凹函数,
有所给图象可知:B:为上凸函数、C为线性函数、D为先凹后凸的函数;
故全部不符合题意.从而只有A适合下凹的性质.
故选A.
| x1+x2 |
| 2 |
| 1 |
| 2 |
∴函数图象在[0,1]上为下凹函数,
有所给图象可知:B:为上凸函数、C为线性函数、D为先凹后凸的函数;
故全部不符合题意.从而只有A适合下凹的性质.
故选A.
点评:此题考查的是函数图象的应用问题.在解答的过程当中充分体现了隐含条件的挖掘、数形结合的思想以及问题转化的能力.值得同学们体会反思.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目

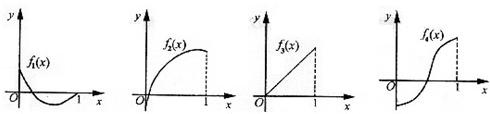
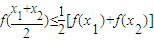 恒成立”的只有( )
恒成立”的只有( )
