设f(x)=6cos2x-2
sinx-cosx,x∈R.
(Ⅰ)求f(x)的最小正周期及单调增区间;
(Ⅱ)若锐角α满足f(a)=3-2
,求tanα及
的值.
| 3 |
(Ⅰ)求f(x)的最小正周期及单调增区间;
(Ⅱ)若锐角α满足f(a)=3-2
| 3 |
| 1+2sinacosa |
| sin2a-cos2a |
已知函数f(x)=ax3+bx2的图象在点(-1,2)处的切线恰好与x-3y=0垂直,又f(x)在区间[m,m+1]上单调递增,则实数m的取值范围是( )
| A、m≤-3 | B、m≥0 | C、m<-3或m>0 | D、m≤-3或m≥0 |
(理)已知双曲线
-
=1的左焦点为F1,左、右顶点为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、相交 | B、相切 |
| C、相离 | D、以上情况都有可能 |
已知0<x<1,a,b为常数且ab<0,则y=
+
的最小值是( )
| a2 |
| x |
| b2 |
| 1-x |
| A、(a+b)2 |
| B、(a-b)2 |
| C、a2+b2 |
| D、|a2-b2| |
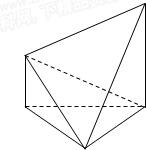 如图,在多面体ABCDE中,DB⊥平面ABC,AE∥BD,且AB=BC=CA=BD=2AE=2
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥BD,且AB=BC=CA=BD=2AE=2