题目内容
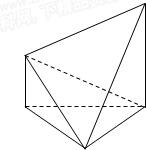 如图,在多面体ABCDE中,DB⊥平面ABC,AE∥BD,且AB=BC=CA=BD=2AE=2
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥BD,且AB=BC=CA=BD=2AE=2(Ⅰ)求证:平面ECD⊥平面BCD
(Ⅱ)求二面角D-EC-B的大小;
(Ⅲ)求三棱锥A-ECD的体积.
分析:(Ⅰ)欲证平面ECD⊥平面BCD,根据面面垂直的判定定理可知在平面ECD内一直线与面CBD垂直,分别取CD、CB的中点F、G,连接EF、FG、AG,易证EF⊥面CBD,又EF?平面ECD,满足定理所需条件;
(Ⅱ)连接BF,过F作FM⊥EC,垂足为M,连接MB,根据二面角平面角的定义可知∠BMF为二面角D-EC-B的平面角,在△ECF中,求出MF,在三角形BMF中求出此角即可;
(Ⅲ)先用等体积法将三棱锥A-ECD的体积转化成三棱锥C-EAD的体积,然后利用三棱锥的体积公式求出所求.
(Ⅱ)连接BF,过F作FM⊥EC,垂足为M,连接MB,根据二面角平面角的定义可知∠BMF为二面角D-EC-B的平面角,在△ECF中,求出MF,在三角形BMF中求出此角即可;
(Ⅲ)先用等体积法将三棱锥A-ECD的体积转化成三棱锥C-EAD的体积,然后利用三棱锥的体积公式求出所求.
解答:解:(Ⅰ)证明:分别取CD、CB的中点F、G,连接EF、FG、AG.
由题知四边形AEFG为矩形,易证AG⊥面CBD,AG∥EF,
∴EF⊥面CBD,
又EF?平面ECD,∴平面ECD⊥平面BCD
解:(Ⅱ)连接BF,则BF⊥CD,由(Ⅰ)知,BF⊥面ECD,过F作FM⊥EC,垂足为M,连接MB,
则∠BMF为二面角D-EC-B的平面角.
由题意知,EC=ED=
,CD=2
,
∴在△ECF中,MF=
=
,又BF=
,
∴tan∠BMF=
=
,
∴二面角D-EC-B的大小为arctan
(Ⅲ)VA-ECD =VC-AED=
S△ADE ×
=
.
由题知四边形AEFG为矩形,易证AG⊥面CBD,AG∥EF,
∴EF⊥面CBD,
又EF?平面ECD,∴平面ECD⊥平面BCD
解:(Ⅱ)连接BF,则BF⊥CD,由(Ⅰ)知,BF⊥面ECD,过F作FM⊥EC,垂足为M,连接MB,
则∠BMF为二面角D-EC-B的平面角.
由题意知,EC=ED=
| 5 |
| 2 |
∴在△ECF中,MF=
| EF•FC |
| CE |
| ||
| 5 |
| 2 |
∴tan∠BMF=
| BF |
| MF |
| ||
| 3 |
∴二面角D-EC-B的大小为arctan
| ||
| 3 |
(Ⅲ)VA-ECD =VC-AED=
| 1 |
| 3 |
| 3 |
| ||
| 3 |
点评:本题主要考查了面面垂直的判定,以及二面角的度量和体积的计算,体积的求解在最近两年高考中频繁出现,值得重视.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC, (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC, (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=