题目内容
甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92(1)求该题被乙独立解出的概率;
(2)求解出该题的人数ξ的数学期望和方差
分析:(1)根据该题被甲独立解出的概率和该题被甲或乙解出的概率,设出事件,表示出概率之间的关系,根据相互独立事件同时发生的概率公式得到结果.
(2)解出该题的人数ξ,由题意知变量的取值可能是0,1,2,根据条件中给出的和第一问解出的概率,写出变量对应的概率,写出分布列、期望和方差.
(2)解出该题的人数ξ,由题意知变量的取值可能是0,1,2,根据条件中给出的和第一问解出的概率,写出变量对应的概率,写出分布列、期望和方差.
解答:解:(1)记甲乙分别解出此题的事件记为A和B
设甲独立解出此题的概率为P1,乙独立解出为P2
则P(A)=P1=06,P(B)=P2
P(A+B)=1-P(
•
)=1-(1-P1)(1-P2)=P1+P2-P1P2=0.92
∴0.6+P2-0.6P2=0.92,则0.4P2=0.32 即P2=0.8
(2)由题意知变量的取值可能是0,1,2,
P(ξ=0)=P(
)•P(
)=0.4×0.2=0.08
P(ξ=1)=P(A)P(
)+P(
)P(B)=0.6×0.2+0.4×0.8=0.44
P(ξ=2)=P(A)•P(B)=0.6×0.8=0.48
∴ξ的概率分布为:

∴Eξ=0×0.08+1×0.44+2×0.48=0.44+0.96=1.4
∴Dξ=(0-1.4)2•0.08+(1-1.4)2•0.44+(2-1.4)2-1.48
=0.1568+0.0704+0.1728=0.4
设甲独立解出此题的概率为P1,乙独立解出为P2
则P(A)=P1=06,P(B)=P2
P(A+B)=1-P(
| A |
| B |
∴0.6+P2-0.6P2=0.92,则0.4P2=0.32 即P2=0.8
(2)由题意知变量的取值可能是0,1,2,
P(ξ=0)=P(
| A |
| B |
P(ξ=1)=P(A)P(
| B |
| A |
P(ξ=2)=P(A)•P(B)=0.6×0.8=0.48
∴ξ的概率分布为:

∴Eξ=0×0.08+1×0.44+2×0.48=0.44+0.96=1.4
∴Dξ=(0-1.4)2•0.08+(1-1.4)2•0.44+(2-1.4)2-1.48
=0.1568+0.0704+0.1728=0.4
点评:本题考查相互独立事件同时发生的概率,考查离散型随机变量的分布列和期望,是一个概率的综合题,解题时注意两问之间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
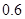 ,被甲或乙解出的概率为
,被甲或乙解出的概率为 ,(1)求该题被乙独立解出的概率;(2)求解出该题的人数
,(1)求该题被乙独立解出的概率;(2)求解出该题的人数 的数学期望和方差
的数学期望和方差 ,被甲或乙解出的概率为
,被甲或乙解出的概率为 ,(1)求该题被乙独立解出的概率;
,(1)求该题被乙独立解出的概率; 的数学期望和方差
的数学期望和方差