设函数f(x)=2
sinxcosx-2sin2x+1(x∈R)，则f（x）的最小正周期为（ ）
| 3 |
| A、2π | ||
| B、π | ||
C、
| ||
D、
|
已知α是第二象限角，且sinα=
，则tan2α=（ ）
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知tanθ=
，则
的值为（ ）
| 4 |
| 3 |
| sinθ+cosθ |
| sinθ-cosθ |
A、
| ||
B、-
| ||
| C、7 | ||
| D、-7 |
函数y=2cos2(x+
)-1的一个单调递增区间是（ ）
| π |
| 4 |
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(-
|
函数y=sin2x+sinxcosx的最小正周期T=（ ）
| A、2π | ||
| B、π | ||
C、
| ||
D、
|
下列命题中真命题是（ ）
| A、y=sin4x-cos4x的最小正周期是π； | ||
B、终边在y轴上的角的集合是{x|x=
| ||
| C、在同一坐标系中，y=sinx的图象和y=x的图象有三个公共点； | ||
D、y=sin(x-
|
已知cos(π+x)=
，x∈(π，2π)，则sinx=（ ）
| 3 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知tanα=-
，则tan(α+
π)的值是（ ）
| 4 |
| 3 |
| 1 |
| 4 |
| A、-7 | ||
B、-
| ||
| C、7 | ||
D、
|
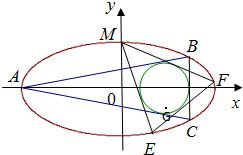如图，已知圆G：（x-2）2+y2=r2是椭圆