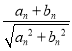【题目】某大学志愿者协会有![]() 名同学,成员构成如下表,其中表中部分数据不清楚,只知道从这
名同学,成员构成如下表,其中表中部分数据不清楚,只知道从这![]() 名同学中随机抽取一位,抽到该名同学为“数学专业”的概率为
名同学中随机抽取一位,抽到该名同学为“数学专业”的概率为![]() .
.
性别 专业 | 中文 | 英语 | 数学 | 体育 |
男 |
|
|
|
|
女 |
|
|
|
|
现从这![]() 名同学中随机抽取
名同学中随机抽取![]() 名同学参加社会公益活动(每位同学被选到的可能性相同).
名同学参加社会公益活动(每位同学被选到的可能性相同).
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求选出的![]() 名同学恰为专业互不相同的男生的概率
名同学恰为专业互不相同的男生的概率
(Ⅲ)设![]() 为选出的
为选出的![]() 名同学中“女生或数学专业”的学生的人数,求随机变量
名同学中“女生或数学专业”的学生的人数,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
【题目】为了解人们对“延迟退休年龄政策”的态度,某部门从年龄在![]() 岁到
岁到![]() 岁的人群中随机调查了
岁的人群中随机调查了![]() 人,并得到如图所示的频率分布直方图,在这
人,并得到如图所示的频率分布直方图,在这![]() 人中不支持“延迟退休年龄政策”的人数与年龄的统计结果如图所示:
人中不支持“延迟退休年龄政策”的人数与年龄的统计结果如图所示:

年龄 | 不支持“延迟退休年龄政策”的人数 |
|
|
|
|
|
|
|
|
|
|
(1)由频率分布直方图,估计这![]() 人年龄的平均数;
人年龄的平均数;
(2)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过![]() 的前提下,认为以
的前提下,认为以![]() 岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
45岁以下 | 45岁以上 | 总计 | |
不支持 | |||
支持 | |||
总计 |
附:![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为“喜爱打篮球与性别有关”?说明你的理由.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 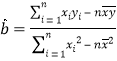 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?