题目内容
【题目】在直角坐标系![]() 中, 椭圆
中, 椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其右焦点为
,其右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
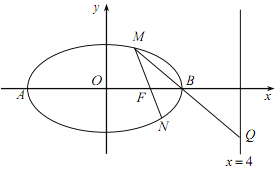
(2)设椭圆的左、右顶点分别为![]() ,
,![]() 是椭圆上异于
是椭圆上异于![]() 的任意一点,直线
的任意一点,直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交直线
交直线![]() 于
于![]() 点, 求证:
点, 求证:![]() 三点在同一条直线上
三点在同一条直线上
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)(法一)由题意,求得椭圆的焦点坐标,利用椭圆的定义,求得![]() ,进而求得
,进而求得![]() 的值,即可得到椭圆的标准方程;
的值,即可得到椭圆的标准方程;
(法二)设椭圆![]() 的方程为
的方程为![]() (
(![]() ),列出方程组,求得
),列出方程组,求得![]() 的值,得到椭圆的标准方程。
的值,得到椭圆的标准方程。
(2)设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立方程组,利用根与系数的关系和向量的运算,即可证得三点共线。
,联立方程组,利用根与系数的关系和向量的运算,即可证得三点共线。
(1)(法一)设椭圆![]() 的方程为
的方程为![]() ,
,
∵一个焦点坐标为![]() ,∴另一个焦点坐标为
,∴另一个焦点坐标为![]() ,
,
∴由椭圆定义可知![]() ,
,
∴![]() ,∴
,∴![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(法二)不妨设椭圆![]() 的方程为
的方程为![]() (
(![]() ),
),
∵一个焦点坐标为![]() ,∴
,∴![]() ,①
,①
又∵点![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,②
,②
联立方程①,②,解得![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由方程组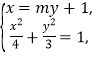 消去
消去![]() ,并整理得:
,并整理得:![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∵直线![]() 的方程可表示为
的方程可表示为![]() ,
,
将此方程与直线![]() 联立,可求得点
联立,可求得点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]()
∵![]()
![]()
![]()
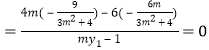 ,所以
,所以![]() ,
,
又向量![]() 和
和![]() 有公共点
有公共点![]() ,故
,故![]() ,
,![]() ,
,![]() 三点在同一条直线上.
三点在同一条直线上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

