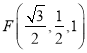【题目】某石化集团获得了某地深海油田区块的开采权.集团在该地区随机初步勘探了部分几口井.取得了地质资料,进入全面勘探时期后.集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高.如果新设计的井位与原有井位重合或接近.便利用旧并的地质资料.不必打这日新并,以节约勘探费与用,勘探初期数据资料见如表:
井号 |
|
|
|
|
|
|
坐标 |
|
|
|
|
|
|
钻探深度 |
|
|
|
|
|
|
出油量 |
|
|
|
|
|
|
(参考公式和计算结果: ,
,![]() ,
,![]() ,
,![]() ).
).
(![]() )
)![]() 号旧井位置线性分布,借助前
号旧井位置线性分布,借助前![]() 组数据求得回归直线方程为
组数据求得回归直线方程为![]() ,求
,求![]() 的值.
的值.
(![]() )现准备勘探新井
)现准备勘探新井![]() ,若通过
,若通过![]() ,
,![]() ,
,![]() ,
,![]() 号井计算出的
号井计算出的![]() ,
,![]() 的值(
的值(![]() ,
,![]() 精确到
精确到![]() )相比于(
)相比于(![]() )中的
)中的![]() ,
,![]() ,值之差不超过
,值之差不超过![]() .则使用位置最接近的已有旧井
.则使用位置最接近的已有旧井![]() .否则在新位置打开,请判断可否使用旧井?
.否则在新位置打开,请判断可否使用旧井?
(![]() )设出油量与勘探深度的比值
)设出油量与勘探深度的比值![]() 不低于
不低于![]() 的勘探井称为优质井,那么在原有
的勘探井称为优质井,那么在原有![]() 口井中任意勘探
口井中任意勘探![]() 口井,求勘探优质井数
口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
【题目】中国政府实施“互联网+”战略以来,手机作为客户端越来越为人们所青睐,通过手机实现衣食住行消费已经成为一种主要的消费方式,“一机在手,走遍天下”的时代已经到来。在某著名的夜市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有
列联表,并根据此资料判断是否有![]() 的把握认为“市场购物用手机支付与年龄有关”?
的把握认为“市场购物用手机支付与年龄有关”?
(2)现采用分层抽样从这100名顾客中按照“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本,设事件![]() 为“从这个样本中任选2人,这2人中至少有1人是不使用手机支付的”,求事件
为“从这个样本中任选2人,这2人中至少有1人是不使用手机支付的”,求事件![]() 发生的概率?
发生的概率?
|
|
|
|
|
|
|
|
|
|
![]() 列联表
列联表
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 24 | ||
合计 | 100 |
附:![]()
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
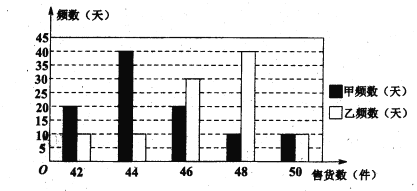
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
【答案】(I)见解析; (Ⅱ)见解析.
【解析】分析:(I)依题意可得甲公司一名推销员的工资与销售件数的关系是一次函数的关系式,而乙公司是分段函数的关系式,由此解得;(Ⅱ)分别根据条形图求得甲、乙公司一名推销员的日工资的分布列,从而可分别求得数学期望,进而可得结论.
详解:(I)由题意得,甲公司一名推销员的日工资![]() (单位:元) 与销售件数
(单位:元) 与销售件数![]() 的关系式为:
的关系式为: ![]() .
.
乙公司一名推销员的日工资![]() (单位: 元) 与销售件数
(单位: 元) 与销售件数![]() 的关系式为:
的关系式为: 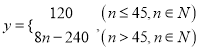
(Ⅱ)记甲公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 122 | 124 | 126 | 128 | 130 |
| 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
记乙公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 120 | 128 | 144 | 160 |
| 0.2 | 0.3 | 0.4 | 0.1 |
∴![]()
∴仅从日均收入的角度考虑,我会选择去乙公司.
点睛:求解离散型随机变量的数学期望的一般步骤为:
第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;
第二步是“探求概率”,即利用排列组合,枚举法,概率公式,求出随机变量取每个值时的概率;
第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;
第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值
【题型】解答题
【结束】
19
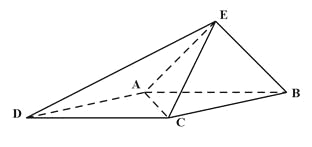
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
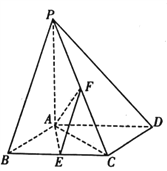
(1)证明: ![]() ;
;
(2)设![]() 为线段
为线段![]() 上的动点,若线段
上的动点,若线段![]() 长的最小值为
长的最小值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.